Definition 38
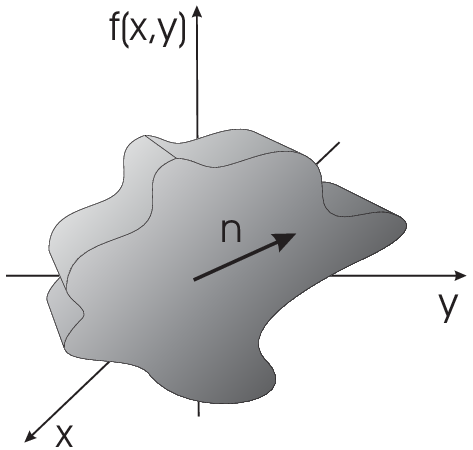
Derivative in certain direction:
is defined as the derivative of \(f\) in the direction \(\vec{n}\)
| 
|
Definition 38
Derivative in certain direction:
is defined as the derivative of \(f\) in the direction \(\vec{n}\)
| 
|
In general: writing \(\vec{n}\) as a linear combination of base vectors, i.e.
| \[\vec{n}=\sum n_i \vec{e}_i\] |
and taking into account, that differentiation is a linear operation we get
| \[ \frac{\partial f}{\partial \vec{n}}= \sum \frac{\partial f}{\partial \vec{e}_i} n_i =\underbrace{\vect{\frac{\partial f}{\partial x_1}\\\vdots\\\frac{\partial f}{\partial x_N}}}_{\begin{array}{c}\mbox{This vector is called}\\\mbox{the gradient of $f$}\end{array}}\cdot\vect{n_1\\\vdots\\n_N}\] |
Definition 39 \(f:\mathbb{R}^N\rightarrow\mathbb{R}\) then gradient is the vector
| \[\vec{\nabla}f=\vect{\frac{\partial f}{\partial x_1}\\\vdots\\\frac{\partial f}{\partial x_N}}\in\mathbb{R}^N\] |
Example: \begin{eqnarray*}f(\vec{x})&=&\sqrt{x_1^2+\ldots+x_N^2}\qquad \frac{\partial f}{\partial x_k}=\frac{x_k}{\sqrt{x_1^2+\ldots+x_N^2}}\\ \rightarrow\,\vec{\nabla}f&=&\frac{1}{\sqrt{x_1^2+\ldots+x_n^2}}\vect{x_1\\\vdots\\x_k}=\frac{1}{|\vec{r}|}\vec{r}\end{eqnarray*}
Derivative in a certain
direction \(\vec{n}\in\mathbb{R}^N\) can be written as:
Thus as illustrated in the figure, the gradient is the direction of steepest descent. | 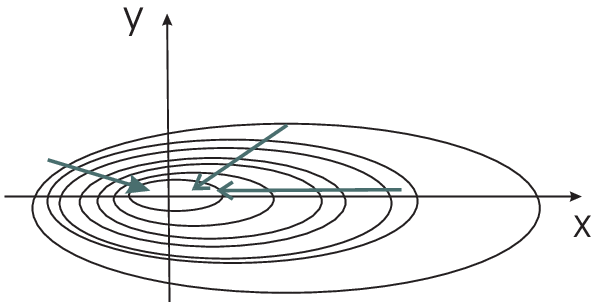
|
| \[ \frac{\partial}{\partial x_k}\left(\frac{\partial f}{\partial x_k}\right)=\frac{\partial^2 f}{\partial x_k^2}\] |
Also possible:
| \[\frac{\partial }{\partial x_j}\left(\frac{\partial f}{\partial x_k}\right)=\frac{\partial^2 f}{\partial x_j\partial x_k}\] |
Always ( apart from mathematically pathological cases):
| \[ \frac{\partial^2 f}{\partial x_j\partial x_k}=\frac{\partial^2 f}{\partial x_k\partial x_j}\leftarrow\,\mbox{exchange order of derivatives doesn't influence the result}\] |
\(n\)-th derivative:
| \[\frac{\partial^n f}{\underbrace{\partial x_k\ldots\partial x_j}_{\mbox{$n$-terms}}}\] |
Examples:
\begin{eqnarray*}f(x_1,x_2)&=&x_1^2+x_2^3\\ \frac{\partial f}{\partial x_1}&=&2x_1\quad,\quad\frac{\partial f}{\partial x_2}=3x_2^2\\ \frac{\partial^2 f}{\partial x_1^2}&=&2\quad,\quad\frac{\partial^2 f}{\partial x_2^2}=6x_2\\ \frac{\partial^2 f}{\partial x_1\partial x_2}&=&0=\frac{\partial^2 f}{\partial x_2\partial x_1}\end{eqnarray*}
\begin{eqnarray*} f(x,y)&=&e^{x^2}y^3\\ \frac{\partial f}{\partial x}&=&2xe^{x^2}y^3\qquad\frac{\partial f}{\partial y}=3y^2e^{x^2}\\ \frac{\partial^2 f}{\partial x^2}&=&2e^{x^2}y^3(1+2x^2)\qquad\frac{\partial^2 f}{\partial y^2}=6ye^{x^2}\\ \frac{\partial^2 f}{\partial x\partial y}&=&6xy^2e^{x^2}\qquad\frac{\partial^2 f}{\partial y\partial x}=6xy^2e^{x^2}\\ \frac{\partial^3 f}{\partial y\partial x^2}&=&6y^2e^{x^2}(1+2x^2)\end{eqnarray*}
© J. Carstensen (Math for MS)