 |
For many mathematical problems, it is far easier to use spherical coordinates
instead of Cartesian ones. |
|
 |
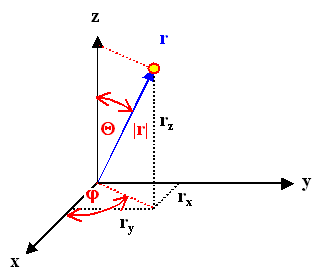
In essence, a vector r (we drop the underlining
here) with the Cartesian coordinates (x,y,z ) is expressed in spherical coordinates by giving its
distance from the origin (assumed to be identical for both systems) |r|, and the two angles j
and Q between the direction of r and the x- and z-axis
of the Cartesian system. |
|
 |
This sounds more complicated than it actually is: j and
Q are nothing but the geographic longitude and latitude. The picture below illustrates this. |
| |
|
 |
This is simple enough, for the translation from one system to the other one we
have the equations |
| |
| x = |
r · sinQ · cosj |
| r = |
(x2 + y2 + z2)½ |
| y = |
r · sinQ · sin j |
| j = |
arctg (y/x) | | z = |
r · cos Q | |
Q = |
arctg |
(x2 + y2 + z2 )½
z |
|
|
 |
Not particularly difficult, but not so easy either. |
 |
Note that there is now a certain ambiguity: You describe the same
vector for an ¥ set of values for Q
and f, because you always can add n·2 p (n = 1,2,3...)
to any of the two angles and obtain the same result. |
|
 |
This has a first consequence if you do an integration. Lets look at the ubiquitous
case of normalizing a wave function y (x,y,z) by demanding that |
| |
¥
ó
õ
–¥ |
¥
ó
õ
–¥ |
¥
ó
õ
–¥ |
y (x,y,z) · dxdydz = 1 |
|
|
 |
In spherical coordinates, we have |
| |
¥
ó
õ
0 |
2p
ó
õ
0 |
p
ó
õ
0 |
y (r,j,Q) · dr
dj dQ = 1 |
|
|
|
 |
You no longer integrate from -¥
to ¥
with respect to the angles, but from 0 to 2p for j
and from 0 to p for Q because this covers all
of space. Notice the different upper bounds! |
 |
Lets try this by computing the volume VR
of a sphere with radius R. This is always done by summing over all the differential volume elements dV
inside the body defined by some equation |
|
 |
In Cartesian coordinates we have for the volume element dV = dxdydz, and
for the integral:
|
| |
¥
ó
õ
–¥ |
¥
ó
õ
–¥ |
¥
ó
õ
–¥ |
??? dxdydz |
|
|
|
 |
Well, if you can just formulate the integral,
let alone solving it, you are already doing well! |
 |
In spherical coordinates we first have to define the volume element. This is relatively
easily done by looking at a drawing of it: |
|
|
|
|
|
 |
An incremental increase in the three coordinates by dr, dj,
and dQ produces the volume element dV which is close enough to a rectangular body
to render its volume as the product of the length of the three sides. |
 |
Looking at the basic geometry, the length of the three sides are identified as
dr, r · dQ, and r · sinQ · dj, which gives the volume element |
|
| |
|
|
| |
| dV | = |
r2 · sinQ · dr · d Q · dj |
|
|
| |
| |
|
 |
The volume of our sphere thus results from the integral |
| |
|
|
|
| Vr = |
¥
ó
õ
0 | 2p
ó
õ
0 |
p
ó
õ
0 |
r2 · sinQ · dr d j dQ = 2p · |
¥
ó
õ
0 | p
ó
õ
0 |
r2 · sinQ · dr d Q =
2p |
· [–cos p + cos 0] · |
¥
ó
õ
0 | r2 · dr |
| Vr = |
2p · | [2] · |
1/3R3 |
= (4/3) · p · R3 |
q.e.d. |
|
|
| |
|
|
 |
Not extremely easy, but no problem either. |
 |
Next, consider differential
operators, like div, rot, or more general, 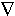 and and 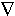 2 (= D). 2 (= D).
|
|
 |
Lets just look at D to see what happens. We
have (for some function U) |
|
| |
| |
| Cartesian coordinates |
| D = |
¶2U
| + |
¶2U
| + |
¶2U
|
| ¶x2 | ¶y2 |
¶z2 |
|
|
| |
|
|
|
| Spherical Coordinates |
| D = |
¶2U
¶r2 | + |
2
r | · |
¶U
¶ r |
+ |
1
r2 · sin2 · Q |
· |
¶2U
¶j2 |
+ | 1
r2 |
· |
¶2U
¶
Q2 | + |
cotg Q
r2 |
· |
¶U
¶Q |
|
|
| |
|
|
 |
Looks messy, OK, but it is still a lot easier to work with this D operator than with its Cartesian counterpart for problems with spherical symmetry; witness the
solution of Schrödingers equation for the Hydrogen
atom. |
 |
Looking back now on our
treatment of the orientation polarization, we find yet another way of expressing spherical coordinates for problems with
particular symmetry: |
|
 |
We use a solid angle
W and its increment dW. |
|
 |
A solid
angle
W is defined as the ratio of the area on a unit sphere that is cut out by a cone with
the solid angle W to the total surface of a unit sphere ( = 4pR2
= = 4p for R = 1). |
|
 |
A solid angle of 4p therefore is the same as the total sphere,
and a solid angle of p is a cone with a (plane) opening angle of 120o
(figure that out our yourself). |
 |
An incremental change of a solid angle creates a kind of ribbon around the opening
of the cone defined by W. This is shown below |
| |
|
 |
Relations with spherical symmetry where the value of Q
does not matter - i.e. it does not appear in the relevant equations - are more elegantly expressed with the solid angle
W. |
|
 |
That is the reason why practically all text books introduce Q
in the treatment of the polarization orientation. And in order to be compatible with most text books, that was what we did
in the main part of the Hyperscript. |
|
 |
Of course, eventually, we have to replace Q and d Q by the basic variables that describe the problem, and that is only the angle d
in our problem (same thing as the angle j here). |
 |
Expressing
dQ in terms of d is easy (compare the picture in the main text) |
|
 |
The radius ot the circle bounded by the dQ ribbon is r·sind = sind because we have the unit sphere, and its width is simply dd. |
|
 |
Its incremental area is thus the relation that we used in the main
part. |
| |
|
| |
|
© H. Föll (Electronic Materials - Script)
![]() 3.2.4 Orientation Polarization
3.2.4 Orientation Polarization