|
|
 |
Startpunkt: |
|
 |
Nur Betrachtung von Grenzen zwischen zwei kristallinen
Phasen. |
|
 |
Im allgemeine existiert kein CSL; da Gittertyp und
Gitterparameter verschieden sind. |
|
 |
Das eventuell vorliegende CSL ist nicht unbedingt das
Bezugsgitter. Beispiel:
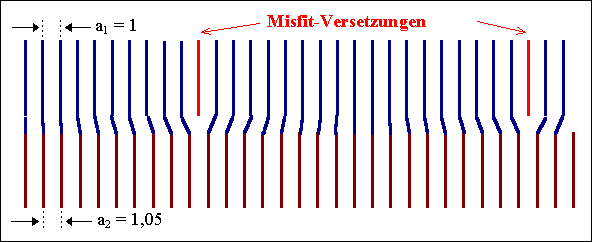
zwei kubische Kristalle mit a1=1; a2=1,05 |
|
|
 |
|
 |
Es ist viel besser, hier eine S=1 Struktur
anzustreben, und dazu einen besonderen Typ von Grenzflächenversetzung
einzuführen; die Misfit-Versetzung.
|
|
|
|
 |
Eigenschaften von
Misfit-Versetzungen |
|
 |
Misfit-Versetzungen konzentrieren die Fehlanpassung
durch verschiedene Gitterparameter auf die Versetzungslinien |
|
 |
Zwischen den Misfit-Versetzungen ist die Grenzfläche
kohärent |
|
 |
Eine Phasengrenze sonst kohärente Phasengrenze mit
Misfit-Versetzungen heißt semi-kohärent |
|
 |
Misfit-Versetzungen müssen immereine
Stufenkomponente haben |
|
 |
Misfit-Versetzungen sind die dominierenden Defekte in den
technisch wichtigen Phasengrenzen; insbesondere in der Optoelektronik |
|
 |
Nur wegen Misfit-Versetzungen kann GaAs nicht auf
Silizium intergriert werden |
|
 |
Viele "Quantum Well" Strukturen leiden unter
Misfit-Versetzungen |
|
 |
Misfit-Versetzungen treten bei dünnen Schichten einer
zweiten Phase auf einem dicken Substrat erst ab einer Mindestschichtdicke auf;
vorher wird die Fehlanpassung elastisch aufgefangen |
8.1.2 Energiebetrachtung zur "kritischen Dicke"
|
 |
Die hier geplante kurze Ableitung der berühmten Formel von
Frank und
van der Merve
entfällt zugunsten einer lehrreichen Kopie aus einem zusammenfassenden
Artikel des vielleicht berühmtesten derzeitigen TEM- und Defektexperten;
|
|
 |
Sir Peter
Hirsch; University Oxford. (Aus "Proc. 2nd Intern. Conf. on
Polycrystalline Semiconductors, Schwäbisch Hall 1990, S. 470ff) |
|
|
Auszug aus Sir
Peters Paper |
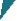 |
Wie man sieht, sind auch große Geister nicht
vor kleinen Fehlern gefeit, denn: |
|
 |
Was ist e? |
|
 |
Was sucht h in der Gleichung für hc? |
|
 |
Wo steckt in Gl. 5 der Versetzungsabstand? |
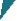 |
Trotzdem, Gl. 5 ist der Spur nach richtig:
Misfit-Versetzungen sind erst ab einer kritischen Dicke hc der Schicht
energetisch günstig, diese krtitische Dicke ist um so
größer |
|
 |
je größer der mögliche Burgersvektor und |
|
 |
je kleiner der Misfit-Parameter f |
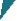 |
Beobachtungen bestätigen dies: Sehr
dünne Schichten haben keine Versetzungen in der Grenzfläche: damit
stellt sich die schwierige und technisch außerordentlich bedeutsame
Frage: |
|
 |
Wie kommen mit wachsender Dicke der
Schicht die Misfit-Versetzungen in die Grenzfläche, und: Wie kann ich
diesen Nukleations- und Wanderungsprozeß möglichst verhindern?
|
8.1.3 Weitere Defekte in Phasengrenzen
|
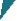 |
Semikohärente Phasengrenzen können
natürlich außer Misfit-Verstzungen noch weitere Defekte
enthalten |
|
 |
kohärente Stufen (ohne Versetzungscharakter) |
|
 |
Netzwerke von Versetzungen, die nach Anpassung der
Gitterparameter durch Misfit-Versetzungen kleine Verdrehungen auffangen, analog
zu Korngrenzen - Versetzungen |
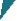 |
Semikohärente Phasengrenzen können auch
S=3 oder andere Koinzidenz-Beziehungen haben |
|
 |
Ein hexagonales Gitter auf der {111} Ebene eines kubischen
Kristalls entspricht einer S=3 Orientierung |
|
 |
Phasengrenzen zwischen kubischen Kristallen auf {111} Ebenen
kommen häufig in der S=1 und
S=3 Orientierung vor. |
|
 |
Es existieren selbstverständlich auch kompliziertere
Geometrien. |
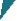 |
Alle Defekte zu sortieren, ist schwierig; die
Interpretation von TEM - Bildern ist nicht mehr einfach. |
|
 |
Beispiele in den Fallstudien |



