S is Always Odd

They most conspicuous issue in the CSL theory of grain boundaries is that there are no even values for S!

Try as you might - you will never find a S = 2 boundary or any other even number in the literature. Now why is this? Mostly no explanation is given.

A rigorous proof essentially needs the full power of the O-lattice theory, so it can not be easily given. But the general reason for this peculiar geometric fact can be envisioned as follows.

First, remember that any grain boundary can be obtained by generating grain II out of grain I by one rotation around a suitable axis with the rotation angle g.

This means that we can produce all CSL orientations by looking at one rotation. We will do this for a square lattice, rotating around a <100> axis.

It is, however, not obvious that we can indeed produce all possible boundaries by this rotation, nor is it clear that the result will be valid for grain boundaries in non-cubic crystals. But it shows the direction of the argument.

From all possible rotation, some will produce CSL structures. Which ones will do that is easily conceived:

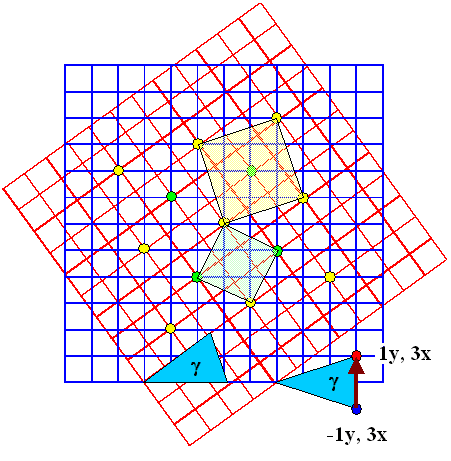
The picture below shows a blue crystal I. Taking its origin at the apex of the blue triangle on the right, we see that we always will get a CSL orientation if we look at lattice points with the coordinates (x, –y₀) which we may express as (n, –1) if we set x₀, y₀ = 1, and than rotate the crystal so the the y-coordinate changes from –1 to +1. The shift is indicated by the bold brown vector; we need to rotate an angle g given by

g	= ½ cotg	y x	= 2 · cotg	1 n

The red lattice has been rotated by just the right amount to move the point (3, –1) to the position (3, +1); the rotation center is in the middle of the crystals

With this procedure we created the yellow CSL lattice.

Its S' value is given by its area divided by the are of a unit cell of the lattice; we have

S'	=	(x² + y²)² x₀ · x₀	=	(3x₀)² + (1x₀)²) x₀²	= (3² + 1²) = 10

Its easy to generalize for CSL sites generated by moving the point (nx, –y) on the (nx,+y) position, we obtain for the S' values

S'(n)	=	n² + 1²

The result will be

S' is an odd number, if n is an even number (The square of an even number is even plus 1 = odd)

S' is an even number, if n is an odd number (The square of an odd number is odd plus 1 = even.)

So we can get even and odd numbers for S????.

Yes - but upon inspection you will find that for n = odd, there is always an additional coincidence point in the center of the lattice defined by the CSL points produced by the rotation, while for even numbers of n this is not the case.

In the picture above this are the green points, and the lattice constant of the CSL lattice is now smaller. The S value in this case is simply

S	=	n² + 1² 2^1/2 · 2^1/2	= S'/2 = an odd number

Instead of a S = 10 boundary, we generated a S = 5 boundary and there are no even S values.

q.e.d. (sort of)

This, of course, is a far cry from a real mathematical proof, but it imparts the flavor of the thinking behind it.

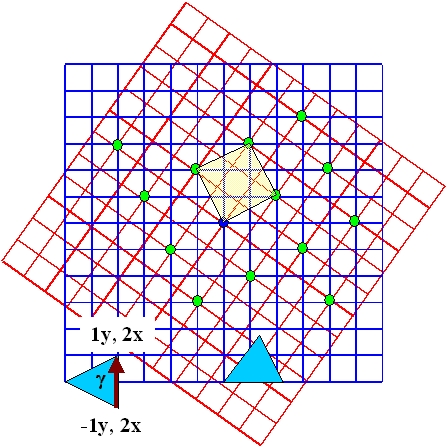
To complete this issue, the following picture shows the result for a rotation that tranfers (2, –1) to (2, +1)

There is no additional coincidenc point and we end up with a S = (n² + 1²) = 5 boundary, the same one as above

With frame

7.1.2 The Coincidence Site Lattice