5.1.3 Essentials to Chapter 5.1: Dislocations

5.1.3 Essentials to Chapter 5.1: Dislocations - Basics

Plastic deformation of crystals=movement of dislocations through the crystal.

The distortion necessary to deform a crystal is localized in a 1-dimensional defect=dislocation that moves through the crystal under the influence of (external shear) forces.

"Discovery" of dislocations as source of plastic deformation=answer to one of the biggest and oldest scientific puzzles in 1934 (Taylor, Orowan and Polyani). No Noble prize!

Movement of dislocations produce steps of atomic size characterized by a vector called "Burgers vector".

Movement of dislocations occurs in a plane (=glide plane) and shifts the upper part of the crystal with respect to the lower part.

Dislocations are characterized by

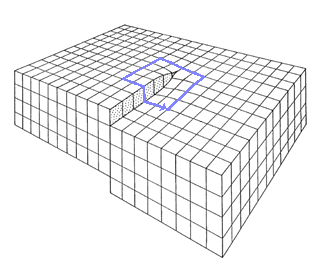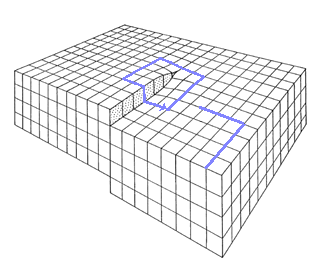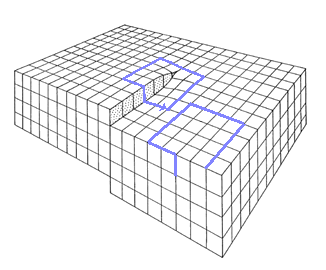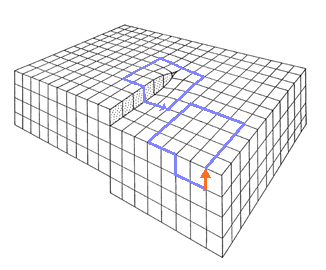Burgers circuit for a screw dislocation

1. Their Burgers vector b=

vector describing the step obtained after a dislocation passed through the crystal.
Vector obtained by a Burgers circuit around a dislocation.
Translation vector in the Volterra procedure.

All definitions of b give identical results for a given dislocations; but watch out for sign conventions!

By definition, b is always a translation vector T of the lattice.

For energetic reasons b is usually the shortest translation vector of the lattice; e.g. b=a/2 <110> for the fcc lattice.

2. Their line vector t(x,y,z) describing the direction of the dislocation line in the lattice

t(x,y,z) is an arbitrary (unit) vector in principle but often a prominent lattice direction in reality

While the dislocation can be curved in any way, it tends to be straight (=shortest possible distance) for energetic reasons.

The glide plane by necessity must contain t(x,y,z) and b and is thus defined by the two vectors

a=90 ^o: Edge dislocation.
a=0 ^o: Screw dislocation.
a=60 ^o: "Sixty degree" dislocation.
a=arbitrary : "Mixed" dislocation.

The angle a between t(x,y,z) and b determines the character or kind of dislocation:

Note that any plane containing t is a glide plane for a screw dislocation.

Dislocations have a large line energy E_dis per length and therefore are never thermal equilibrium defects

E_dis » 5 eV/|b|

The formal Volterra definition of dislocations is very useful and extendable to more complex kinds of dislocations

Volterra definition of screw dislocation

Cut into the lattice with a fictitious "Volterra" knife (make a plane cut to keep it easy), The cut line is a closed loop by necessity. The part of the cut line inside the crystal identifies the dislocation line.

Move the part of the lattice above (or below - attention, signs change!!) the cut plane by an arbitrary lattice translation vector=Burgers vector of the dislocation. Add or remove lattice points as necessary (=remove or fill in atoms in the crystal going with the lattice).

Mend the lattice (or crystal) by "welding the upper part to the lower one. There will be a perfect fit by definition everywhere except along the dislocation line.

Make the best arrangement of the atoms along the dislocation line by minimizing their energy (make best possible bonds).

You now have formed a dislocation.

The procedure is "easily" extended to dislocations in n-dim. lattices, to (special) dislocations with a Burgers vector not defined as translation vector of the lattice and to lattices more complex than a simple crystal lattice.

Direct consequences are:

A dislocation cannot just end in the interior of a crystal

There is a "knot rule" for dislocation knots:
Sb=0
provided the signs of the line vectors follow a convention (all pointing to or away from the knot)

There can be all kinds of dislocation loops (just confine your fictitious cut to the lattice interior!)

Note: "Simple" geometric considerations allow to deduce a lot about properties of dislocations