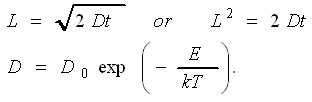
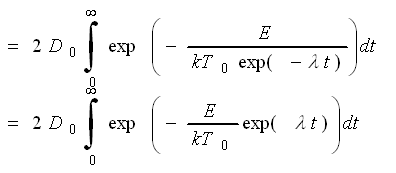
t = 0 changes to u0 = E/kT0
t = ¥ changes to u = ¥.
This gives us
| For the diffusion length L we have the well known equations: | ||
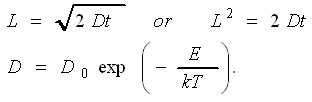 |
||
| E is the activation energy of the diffusing species an k is the Boltzmann constant. Because of T = T0 · exp –(l · t) we obtain for L2 | ||
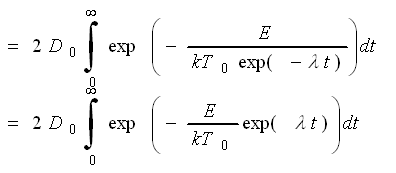 | ||
| Now we have a purely mathematical exercise which is not too difficult, but not too easy either. In order to solve the integral, we try the substitution | ||
| The boundaries must be changed too, we obtain t = 0 changes to u0 = E/kT0 t = ¥ changes to u = ¥. This gives us | ||
| Now you must solve a simple looking integral. There are several ways of doing that | |||||||||||
| |||||||||||
| Here we go the second route. | |||||||||||
| We use a Taylor expansion for 1/u around u0 because that's where u is felt most critically - for large values of u everything tends to be zero anyway. In full generality we have | |||||||||||
| If we keep it really simple, we could just use the first term, having 1/u » 1/u0; but we will go one step beyond this and take | |||||||||||
| |||||||||||
| This gives us | |||||||||||
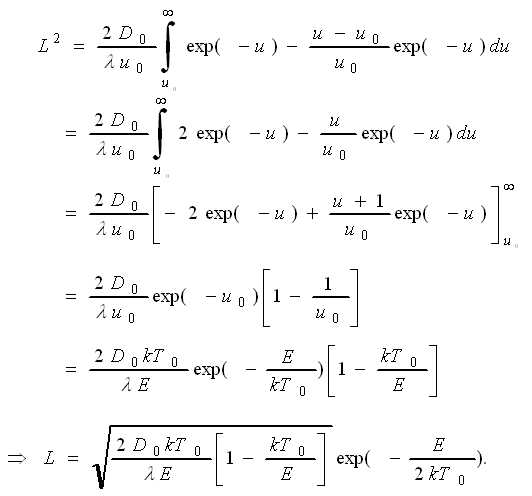 |
|||||||||||
| The second term of the Taylor expansion brought in the factor [1 – kT0/E] and since kT0 « E in all normal cases, it is indeed not very important. If we neglect it, we may simply give the desired solution as | |||||||||||
| |||||||||||
| Now we can look at some typical cases and see what this formula means. However, first we have to find the right values for l | |||||||||||||
| For this we have to take the given values of the initial cooling rate, which we call l', and see what l values correspond to these cooling rates. | |||||||||||||
| The initial cooling rate l' is the derivative of the T(t) function at t = t0 = 0, we thus have | |||||||||||||
| |||||||||||||
| and obtain | |||||||||||||
| |||||||||||||
| The "–" sign cancels, because our l' must carry a minus sign, too, if it is to be a cooling and not a heating rate. | |||||||||||||
| Replacing l by l'/T0 yields the final formula: | |||||||||||||
| |||||||||||||
| We have to evaluate this formula for cooling rates l' given as (–) 1 oK/s, 10 oK/s, 50 oK/s, 104 oK/s, and activation energies of E = 1.0 eV, 2.0 eV, 5 eV. For D0 we take D0 = 10–5 cm2s–1. | |||||||||||||
| The result (including the [1 – kT0/E] term is shown below | |||||||||||||
| |||||||||||||
| What can we learn from the formula and the curves? | |||||||||||||
| |||||||||||||
What can we do with the numbers? Quite simple:
| |||||||||||||
![]() Exercise 4.2-1 Diffusion During Cooling
Exercise 4.2-1 Diffusion During Cooling
![]() Exercise 4.1-1 Lifetime of Positrons
Exercise 4.1-1 Lifetime of Positrons
© H. Föll (Defects - Script)