 |
1. question:: A light beam with intensity I0
passes through one ideal polarizer. |
|
 |
1. How does the intensity relate to the electrical field strength? |
| |
 |
Intensity neasures the energy or better power flux contained in the
light. it is propotional to the square of the electrical field strength |
| | | |
|
 |
2. The incoming ("input") light beam is unpolarized. How large is the intensity
at the output? |
|
 |
It's obviously I0/2. Considering this
picture we can decompose the light beam in two fully polarized beams, each having the intensity I0/2.
The polarizer takes out one of the beams and I0/2 remains. |
| | | |
|
 |
3. Does this intensity change if you rotate the polarizer around the axis coinciding with
the propagation direction of the light = optical axis? |
|
 | No. |
| | |
|
|
 |
4. The incoming light beam is 100 % linearly polarized. How large is the intensity
on the output as a function of the angle between polarization direction of the light and polarizing direction of the polarizer. |
|
 |
The intensity must vary betwen 100 % and 0 % of the incoming intensity for an angle of a = 0o and 90o , respectively.
For an arbitrary angle
a we have a field strength
E(a) = E0 · cosa; the transmitted
intensity then scales with (cosa)2 between the extremes. |
| | |
|
| |
2. question:A light beam with intensity I0
first passes through one ideal polarizer, and then through a second one. Both polarizers
can be rotated freely around the optical axis. |
| |
 |
1. The light beam is unpolarized. How large is the intensity on the output if both ideal
polarizers are in parallel? |
| |
 |
It's still
I0/2 because two polarizers in parallel behave just like one. |
| | | |
|
 |
2. The light beam is unpolarized. How large is the intensity on the output if the ideal
polarizers are "crossed", i.e. their polarization directions are at right angles? |
| |
 |
The intensity is zero. |
| |
| |
|
 |
3. The light beam is 100 % linearly polarized. How large is the intensity of the
output as a function of the variable angle a between the two polarizing directions of
the polarizers and the fixed angle b between the polarization direction of the light and
the first polarizer it encounters? Note that in this case you rotate the second polarizer. |
|
 |
After passing through the first polarizer, the intensity is I0 · (cosb)2.
After passing through the second polarizer we have I = I0 · (cosb)2
· (cosa)2 |
| | | |
|
 |
4. Does the result for the question above change if you rotate the first
polarizer and keep the second one at the fixed angle b? |
| |
 | No. |
| |
|
 |
5. Is for all of the above the direction of the light paths always reversible as stated before? |
|
 |
Tricky. Just reversing arrowheads obviously doesn't work.
You can't get a higher intensity from a
lower one as you would if you just reverse the sign of the Poyntig vector as shown below.
Using a mirror symmetry works but this trival.
|
| | |
|
| |
|
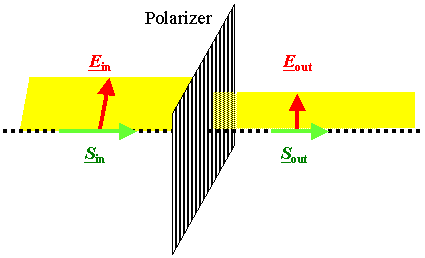
Starting situation.
|
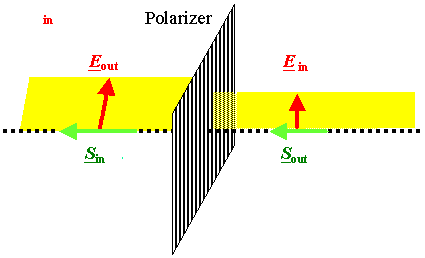
Reversing vector signs does not work. |
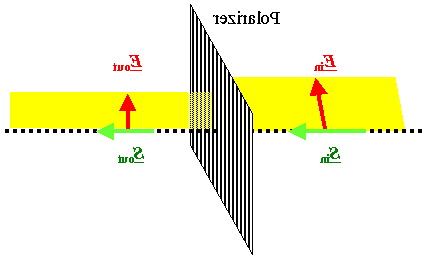
Mirroring
works. |
|
| | |
|
 |
3. question: Now consider a system with two
fixed crossed polarizers and a third one that can
be rotated in between the two crossed ones. |
|
 |
1. The incoming light beam is unpolarized. How large is the intensity of
the output as a function of the variable angle a between the first (fixed) and the third
polarizer that can be rotated? |
|
 |
After the first polarizer, the intensity is I0/2;
it decreases with (cosa)2 behind the third polarizer that can be rotated .
The second (fixed and crossed with respect to the first one) polarizer transmits components with a (sina)2
dependence (make a simple drawing and do the geometry!) so all together we have for the output |
| | |
|
| |
|
| I (a) = |
I0
2 | · |
(cosa)2 · (sina)2 |
| I (a = 0o) = 0 |
| I (a = 45o) = maximal value = (I0/2)
· 0,25 |
| I (a = 90o) = 0 |
|
| | |
|
| |
 |
2. The incoming light beam is 100 % linearly polarized. How large
is the intensity on the output as a function of the variable angle a between the first
(fixed) and the third polarizer (can be rotated) considering that the angle b between
the incoming light polarization and the polarization direction of the first polarizer is fixed at a value b? |
| |
 |
As above except that the intensity after the first polarizer is now I0
· (cosb)2 |
| |
| |
© H. Föll (Advanced Materials B, part 1 - script)


