Binary ideal systems of liquid and gas: x,y- diagrams

2.5 Binary ideal systems of liquid and gas: x,y- diagrams

We now discuss mixtures of \(A\) and \(B\) in liquid and vapor phases. Let \(x_A\) and \(y_A\) be the mole fraction of \(A\) in liquid and vapor phase, respectively. Common sense suggests that the vapor should be richer in the more volatile component (that with larger pure vapor pressure \(p^*\)). In what follows we will confirm this expectation. Let \(p_A^*\) and \(p_B^*\) be the vapor pressures of both pure components. For the liquid we assume Raoult’s law

\begin{equation*} p=p_A + p_B = x_A p_A^* + x_B p_B^* = p_B^* + (p_A^* - p_B^*) x_A \label{p_tot} \quad . \end{equation*}

(2.47)

For the vapor we find from Dalton’s law

\begin{equation*} y_A = \frac{p_A}{p} \quad \mbox{and} \quad y_B = \frac{p_B}{p} \label{y_vapor_1} \end{equation*}

(2.48)

which combining with Eq. (2.47) leads to

\begin{equation*} y_A = \frac{x_A p_A^*}{p_B^* + (p_A^* - p_B^*) x_A} \quad \mbox{and} \quad y_B = 1 - y_A \label{y_vapor_2} \end{equation*}

(2.49)

Just by rearranging we get

\begin{equation*} y_A \left(p_B^* + (p_A^* - p_B^*) x_A \right) = x_A p_A^* \quad \mbox{, i.e.} \quad y_A p_B^* = x_A \left( p_A^* + (p_A^* - p_B^*) y_A\right) \label{y_vapor_3} \end{equation*}

(2.50)

and finally

\begin{equation*} x_A = \frac{y_A p_B^*}{p_B^* + (p_B^* - p_A^*) y_A}\label{x_vapor_1} \end{equation*}

(2.51)

Using Eq. (2.48) we get

\begin{equation*} p = \frac{p_A}{y_A} = \frac{x_A p_A^*}{y_A} \label{p_tot_2} \quad, \end{equation*}

(2.52)

i.e.

\begin{equation*} p_r:=\frac{p}{p_A^*} = \frac{p_B^*}{p_A^* + (p_B^*-p_A^*)y_A } \label{p_r} \quad, \end{equation*}

(2.53)

Figure 2.6: a) Curves for Eq. (2.49) when \(A\) is more volatile then \(B\). b) Curves for Eq. (2.49) when \(B\) is more volatile then \(A\). c) Curves for Eq. (2.53) for several values of \(p_{ratio} = p_A^* / p_B^*\)

Note that all results depend decisively on the ratio \(p_A^* / p_B^*\). Examples for curves representing Eq. (2.49) and Eq. (2.53) are shown in Fig. 2.6.

Figure 2.7: The dependence of the total vapor pressure of an ideal solution on the mole fraction of \(A\) in the entire system. A point between the two lines corresponds to both liquid and vapor being present.

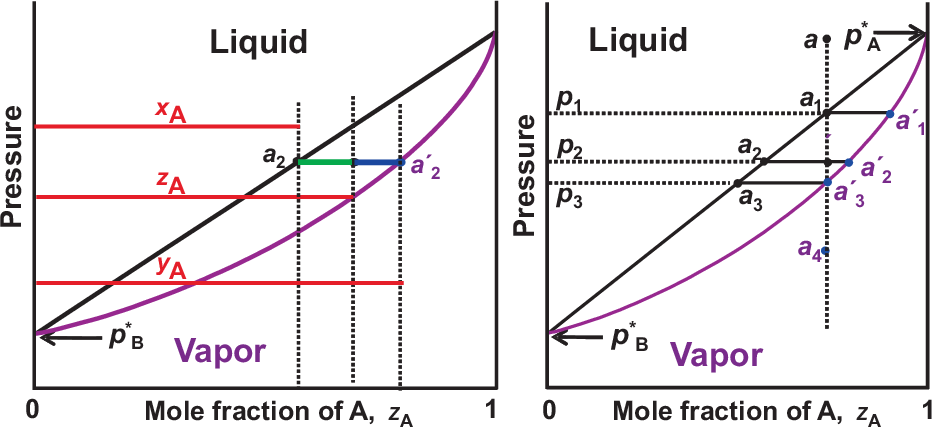
Fig. 2.7 summarizes this results. The straight line separating the liquid phase corresponds to Raoult’s law. The curvature in the line separating the pure vapor phase is a pure entropy effect (ideal case). We now introduce the overall composition \(z_A\). It equals \(z_A = x_A\) if only liquid exists. It equals \(z_A = y_A\) if only gas exists. A point between the two lines corresponds to both liquid and vapor being present. In this region we find for the relative amounts \(n\), \(n(l)\), and \(n(g)\)

\begin{equation*} n z_A = n(l) x_A + n(g) y_A \label{n_z_A_1} \quad . \end{equation*}

(2.54)

Additionally holds

\begin{equation*} n = n(l) + n(g) \quad \mbox{i.e.} \quad n z_A = n(l) z_A + n(g) z_A \label{n_z_A_2} \quad . \end{equation*}

(2.55)

Combining Eq. (2.54) and Eq. (2.55) we get the lever rule

\begin{equation*} \frac{n(l)}{n(g)} = \frac{z_A - y_A}{x_A-z_A} \label{lever_rule} \quad . \end{equation*}

(2.56)

So the horizontal line in Fig. 2.7, e.g. between \(a_2\) and \(a'_2\), describes a phase separation between a liquid and a vapor phase, where the concentration \(y_A\) in the vapor is higher than the overall concentration \(z_a\) due to the higher partial pressure \(p_A^*\) (i.e. \(A\) is more volatile).