Stability and infinitesimal fluctuations

5.16 Stability and infinitesimal fluctuations

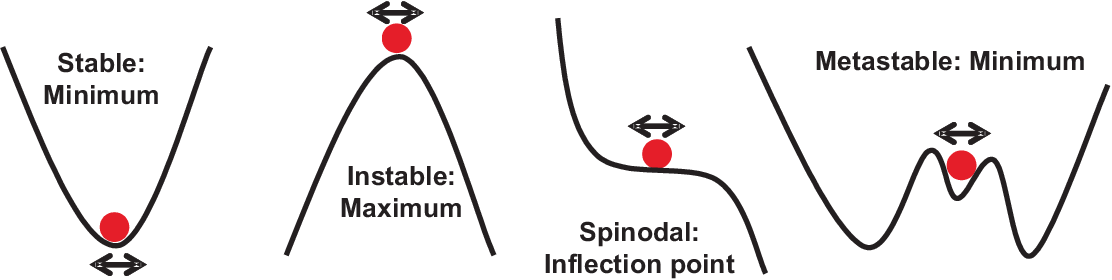
Before discussing the relation between chemical potentials, phase diagrams, and chemical reaction in the next chapters we will briefly summarize some properties of the Gibbs potential which define the stability of thermodynamic equilibrium states in general. In a nutshell thermodynamics and kinetics are the description of a system in equilibrium for different energy landscapes. This is schematically illustrated in Fig. 5.15. analogous to a ball in equilibrium for different landscape scenarios the shape of the Gibbs potential around an equilibrium position defines the effect of infinitesimal positional fluctuation $\xi$. Often $\xi$ is an infinitesimal fluctuation of $p$, $T$, or $n$, respectively. As an example we will discuss a phase change induced by a reaction A $\rightarrow$ B. For a quantitative discussion of stability we introduce the affinity $A = \mu_A - \mu_B$. Using $G = n_a\, \mu_A+ n_B \, \mu_B$ we will loose $\mu_A$ and gain $\mu_B$ in the Gibbs potential for each mole of A which reacts into B ; thus $-A$ is the change in the Gibbs potential related to the chemical reaction. Using the Taylor series expansion of the Gibbs potential we get

\begin{equation*} -A(\xi) = \left(\mu_B - \mu_A\right)(\xi) = \left(\frac{\partial G}{\partial \xi}\right)_{\xi=0} \xi + \frac{1}{2!}\left(\frac{\partial^2 G}{\partial \xi^2}\right)_{\xi=0} \xi^2 + \frac{1}{3!}\left(\frac{\partial^3 G}{\partial \xi^3}\right)_{\xi=0} \xi^3 + \cdots + \frac{1}{n!}\left(\frac{\partial^n G}{\partial \xi^n}\right)_{\xi=0} \xi^n \label{eq:Taylor_affinity} \end{equation*}

(5.53)

Since in equilibrium $G$ is minimal $A = 0$ means no spontaneous change of state, i.e. the stable state. If $A \gt 0$ spontaneous transformation of A into B will happen; correspondingly $A \lt 0$ means spontaneous transformation of B into A.

Figure 5.15: Four Gibbs potential landscapes with affinity zero representing different types of stability.

The four states in Fig. 5.15 behave differently when applying infinitesimal fluctuations in $\xi$: ”stable” means stable against all infinitesimal fluctuations, ”instable” will change by any infinitesimal fluctuation and is stabilized by movement in both directions, ”spinodal” is stabilized by movement in one direction, ”metastable” is locally stable, but does not represent the absolute minimum in energy. Let us quantify this

\begin{equation*} \begin{split} \left(\frac{\partial G}{\partial \xi}\right)_{\xi=0} &=\;\; 0 \quad \mbox{Equilibrium case $\Rightarrow$ sign of $A$ determined by higher order derivatives of $G$}\\ \mbox{and}\quad\left(\frac{\partial^2 G}{\partial \xi^2}\right)_{\xi=0} & \gt \;\; 0 \quad \mbox{Stable and metastable equilibrium case: $A \lt 0$}\\ \left(\frac{\partial^2 G}{\partial \xi^2}\right)_{\xi=0} & \lt \;\; 0 \quad \mbox{Unstable equilibrium case: $A \gt 0$}\\ \left(\frac{\partial^2 G}{\partial \xi^2}\right)_{\xi=0} &=\;\; 0 \quad \mbox{Spinodal equilibrium $\Rightarrow$ sign of $A$ determined by} \; \left(\frac{\partial^3 G}{\partial \xi^3}\right)_{\xi=0} \\ \end{split} \label{eq:stability} \end{equation*}

(5.54)

The first derivate MUST be zero because the discussion is limited to equilibrium cases, thus the higher derivatives determine the sign of $(-A)$. The influence of the second derivative on the sign of $(-A)$ is much larger compared to the third derivative since the fluctuation $\xi$ is assumed to be small, i.e. $(\xi^2 \gg \xi^3)$.

Figure 5.16: Compositional fluctuations.

We use Fig. 5.16 to discuss the relation between the Gibbs potential $G$ and compositional fluctuations. For $T_2$ the points $x_1$ and $x_2$ have the same chemical potentials $(\mu_a = \mu_B)$. This defines the binodal between which phase separation occurs. To discuss compositional fluctuations we assume a fluctuation of the chemical composition by moving slightly up and down from a compositional point of a phase. Green point represents the starting point of fluctuation (just arbitrarily selected examples), red points represent the fluctuation amplitude in the composition. The average value of $G$ for such fluctuation is represented by the LINE connecting the left and right composition point.

At point I) (binodal case) the average $G$ of the locally heterogeneous system (red points and red line) is higher than $G$ of the homogeneous phase with fluctuation. Thus the initial phase is at least in the average more stable than the demixed system. Thus the initial phase is metastable. So $\partial G^2/\partial x_B^2 \gt 0$ implies metastable states against fluctuation inside the homogeneous phase.
At point II) (spinodal case) the average $G$ of the locally heterogeneous system is lower than $G$ of the homogeneous phase with fluctuation. Thus $\partial G^2/\partial x_B^2 \lt 0$ implies unstable states against fluctuation inside the homogeneous phase.

In summary the curvature determines whether the average value due to compositional fluctuation is lower and higher than the one of the initial phase, respectively. Thus, the inflection point of the $G$-curve separates metastable and instable scenarios. Thus a further critical point exists if the third derivative is zero.