Figure 5.4:
Volume of mixing and partial molar volume of solute B: \(dV/dx_b\).
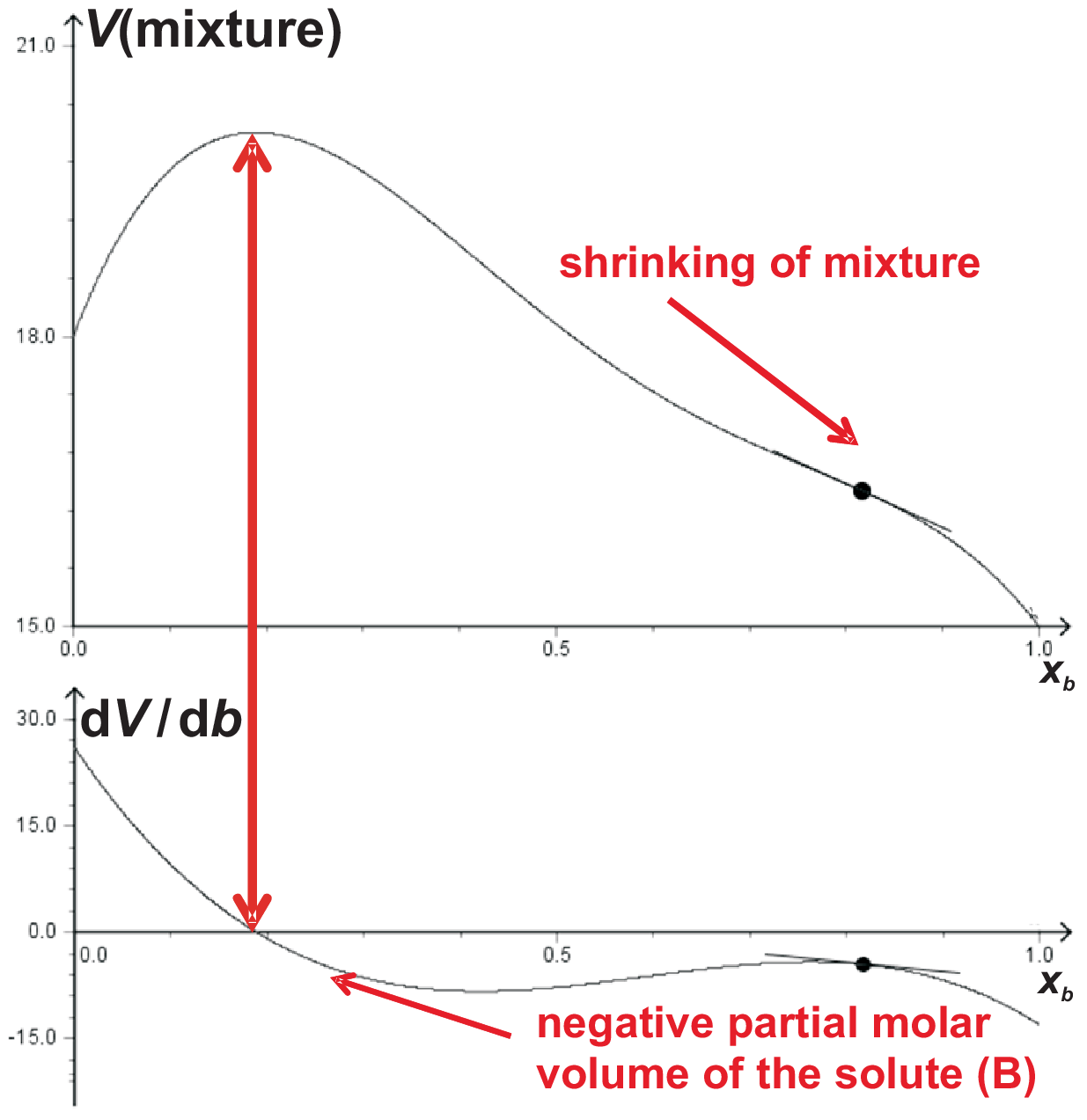
As shown in Fig. 5.3 a) partial molar volumes can also be negative, e.g. for salts which decrease the volume
of a solution when added. The partial volumes represent the slope in Fig. 5.3 a). At point b, the partial molar volume is negative.
The mathematical procedure
for analyzing the partial molar volume and some general explanation for the occurrence of a negative partial molar volume
we will discuss using the curves of Fig. 5.4.
Of course the decreasing volume (shrinking) of the mixture when adding the solute (B) is interrelated with negative values
of the partial molar volumes.
The (systematic) volume enhancement at low \(b\)=[B] can be interpreted as follows: for low [B] the mixture behaves almost ideal, thus there must be an increase in volume when adding B into A.
The standard interpretation for the shrinkage is: the ”open” structure of water (cf. H-bonding) is more and more disturbed, more and more water molecules are arranged with high coordination numbers around solved ions, thus leading to a volume reduction.
\(V(mixing)\) is experimentally treated by putting into A (solvent) variable amounts of B (solute) and measuring the volume of the mixture as shown in Fig. 5.4
step: The measured data \(V(n_B)\) is fitted to a polynomial function
|
| \begin{equation*} V_{p,T}(n_B) = a_0 + a_1\, n_B + a_2\, n_B^2 + a_3 \, n_B^3 \label{eq:polfit_V} \end{equation*} | (5.14) |
step: the partial molar \(V\) of B is calculated by differentiation
|
| \begin{equation*} \left(\frac{\partial V}{\partial n_B} \right)_{p,T,n_A} = a_1 + 2\, a_2\, n_B + 3 \, a_3 \, n_B^2 \label{eq:d_polfit_V_B} \end{equation*} | (5.15) |
step: now the partial molar \(V\) of A can be calculated from
equation discussed below: the maxima are found at the same position but with opposite slopes. |
 |
 |
 |
© J. Carstensen (TD Kin I)