Extensive properties of mixtures: Volume of mixtures and partial molar volume

5.5 Extensive properties of mixtures: Volume of mixtures and partial molar volume

For the condition described by the Gibbs potential the partial molar volume \(dV_{p,T}\) is defined by the total derivative

\begin{equation*} \begin{split} V = V(p,T,n_i) &\Rightarrow \;\; dV = \left(\frac{\partial V}{\partial p} \right)_{T,n_i} dp + \left(\frac{\partial V}{\partial T} \right)_{p,n_i} dT + \sum_i \left(\frac{\partial V}{\partial n_i} \right)_{p,T,n_{j \neq i}} dn_i\\ & \Rightarrow \;\; dV_{p,T} = \sum_i \left(\frac{\partial V}{\partial n_i} \right)_{p,T,n_{j \neq i}} dn_i\\ \label{eq:part_mol_V} \end{split} \end{equation*}

(5.10)

The usage of the partial molar volume becomes clear from the following consideration. First we have to state that \(V\) is a homogeneous function (of first degree), i.e. if the number of the particles of all components is multiplied by \(\alpha\), the volume is multiplied by \(\alpha\):

\begin{equation*} V_{p,T}(\alpha n_1, \alpha n_2, \cdots) = \alpha V_{p,T}(n_1, n_2, \cdots) \label{eq:V_hom_1} \end{equation*}

(5.11)

(so, if e.g. doubling all particle numbers the system will obviously occupy the double volume, i.e. \(V_{p,T}\) is homogeneous in first order). We can now calculate the derivative with respect to \(\alpha\) in Eq. (5.11); applying the chain rule we get

\begin{equation*} \sum_i \left(\frac{\partial V_{p,T}}{\partial \alpha n_i} \right)_{n_{j \neq i}} \frac{d(\alpha n_i)}{d \alpha} = V_{p,T}(n_1, n_2, \cdots) \label{eq:V_hom_2} \end{equation*}

(5.12)

Since Eq. (5.12) holds for all \(\alpha\) we find for \(\alpha = 1\)

\begin{equation*} \sum_i \left(\frac{\partial V_{p,T}}{\partial n_i} \right)_{n_{j \neq i}} n_i = V_{p,T}(n_1, n_2, \cdots) \quad \mbox{or} \quad V_{m,p,T} = \sum_i x_i \left(\frac{\partial V_{p,T}}{\partial n_i} \right)_{n_{j \neq i}} \label{eq:V_hom_3} \end{equation*}

(5.13)

So the \(V(mixture)\) = sum of the partial molar volumes \(\times\) no particles for each component. The right hand version of this equation holds for molar volumes.

Figure 5.3: a) \(V(mixture)\) vs. concentration; b) partial molar volumes of water and ethanol.

The volume of an ideal or heterogeneous mixture is \(V = \sum_i n_i V_{m,i} \)
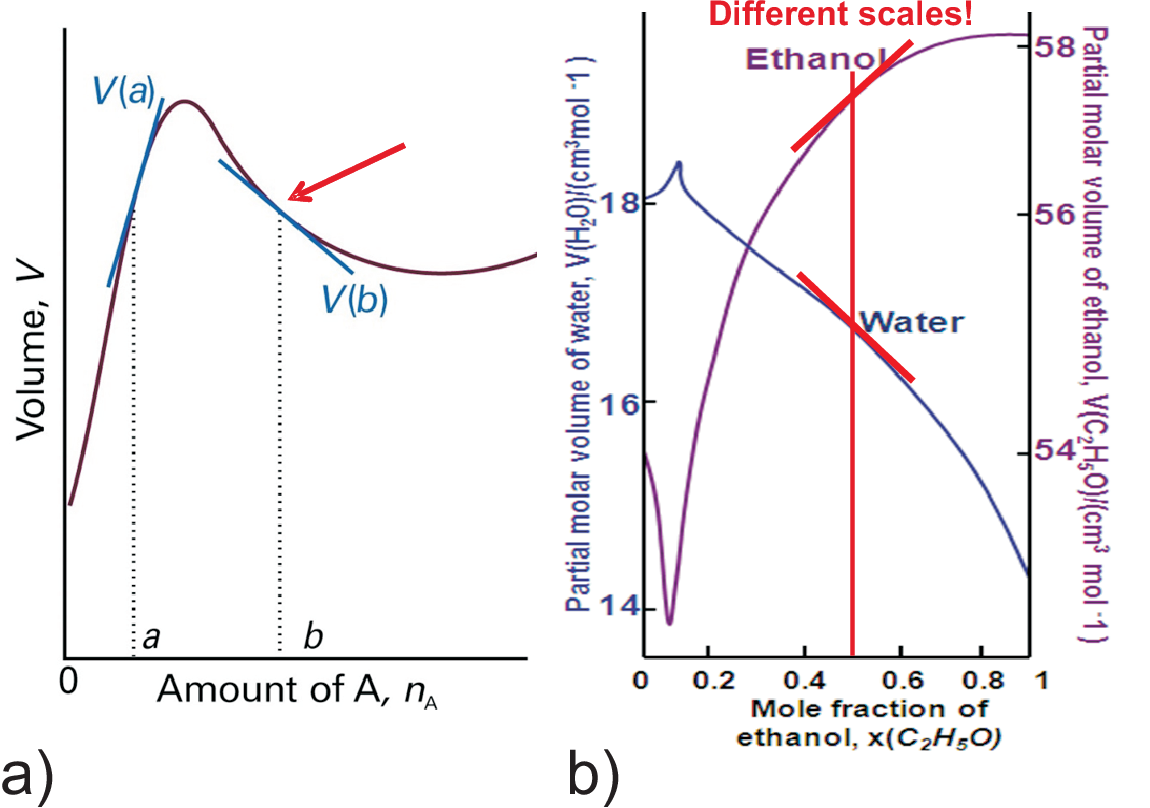
The volume of a real mixture depends on intermolecular forces, e.g. 1 ml ethanol + 1 ml water \(\neq\) 2 ml vodka! The mixing of ethanol and water gives about 1.92 ml. On a molecular scale this is interpreted by attractive forces dominant in the mixture, in terms of a more dense packing of the ethanol molecules (better H-bonding by water).
As a workaround the partial molar volumes are used which can be summed up (cf. ideal case) to give the volume of the mixture.

As an example we calculate the molar volume of a 50 at% EtOH [cm\(^3\)/mol] mixture of water and ethanol. According to Fig. 5.3 b) the partial molar volumes of the pure substances are 18 for water and 58 for ethanol. Assuming an ideal mixture we get
\(V(molar, mixture)\) = (0.5 \(\times\) 18) + (0.5 \(\times\) 58) = 38
Using the values for 50% we get the real value
\(V(molar,mixture)\) = (0.5 \(\times\) 16.8) + (0.5 \(\times\) 57.5) = 37.2
This volume reduction is a general finding: Except for very high water concentrations (left side) both molar partial volumes are always smaller compared to the molar volume of the pure states (18 and 58). Thus the volume of the mixture is always smaller than that of the ideal mixture.