Principle dependence of G on T and p

3.33 Principle dependence of \(G\) on \(T\) and \(p\)

We now use the two partial derivatives of the Gibbs potential to describe the principle \(T\) and \(p\) dependence of the Gibbs potential:

\begin{equation*} \left( \frac{\partial G}{\partial T }\right)_p = - S \quad \mbox{and}\quad \left( \frac{\partial G}{\partial p }\right)_T = V \label{eq:dG_dT_dp} \end{equation*}

(3.85)

Figure 3.11: a) Principle temperature dependence of the Gibbs potential; b) Principle pressure dependence of the Gibbs potential.

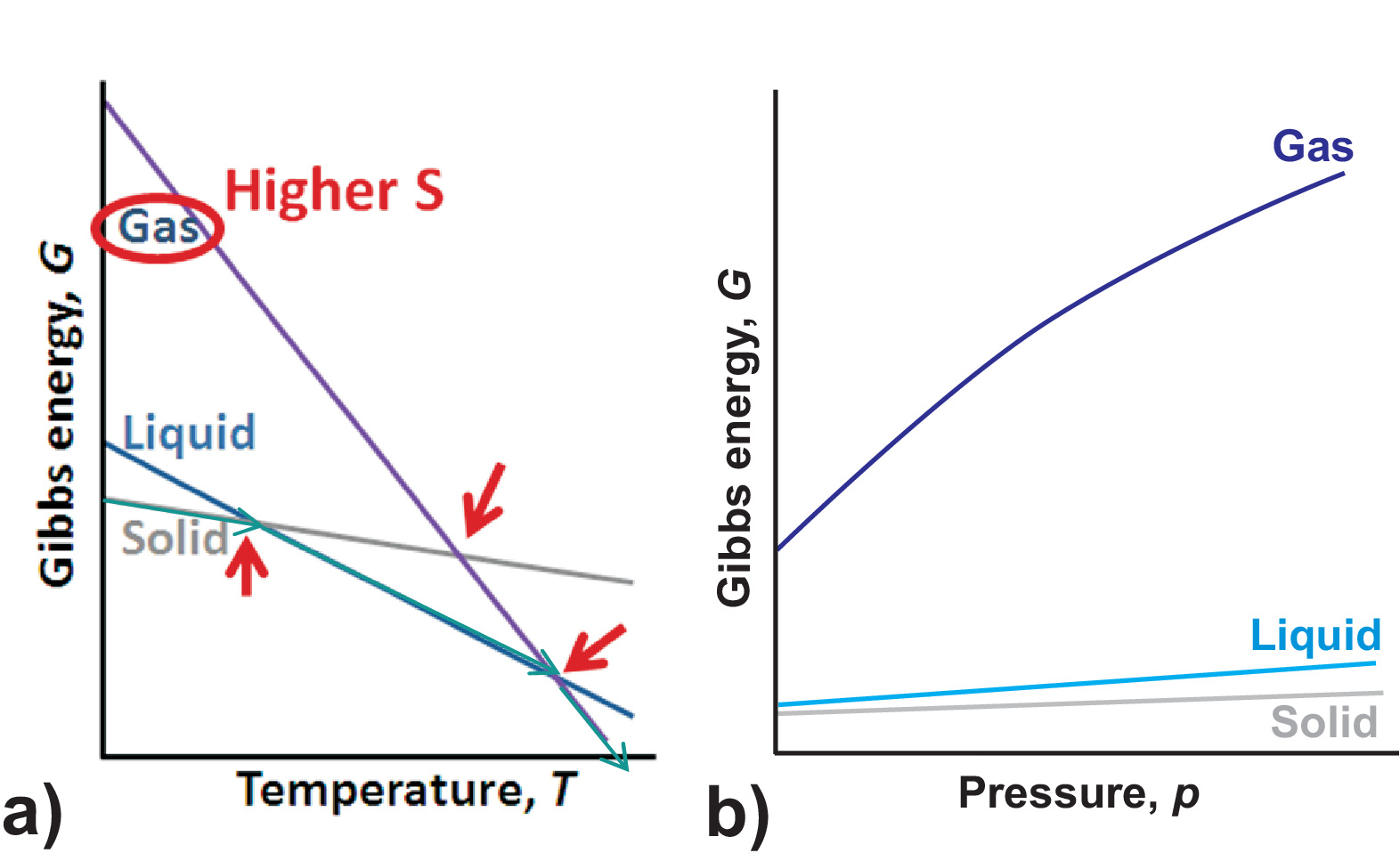
Since the entropy describes the disorder within the system we clearly find \(S(solid) \lt S(liquid) \lt S(gas)\). At low temperature the enthalpy/inner energy of the solid is smaller that that of a liquid which again is smaller that that of a gas. Combining these two statements the principle temperature dependence of the Gibbs potential is shown in Fig. 3.11 a). The intersection points between the three straight lines indicate the melting resp. boiling temperature.
Having larger disorder typically a system needs more volume, so \(V(solid) \lt V(liquid) \lt V(gas)\), where especially the gas phase occupies a much larger volume than the liquid or the solid phase. Thus a principle pressure dependence of the Gibbs potential as shown in Fig. 3.11 b) is found.