Fugacity: Definition and relation to residual function

3.31 Fugacity: Definition and relation to residual function

We will now discuss the fugacity as a parameter to describe the behavior of real gases/fluids. Actually the underlying concept is quite general in materials science since the fugacity \(f\) can be interpreted as an ”effective pressure” much the same as e.g. effective masses are used to describe properties of real (non-free) electrons. First we have to find the pressure dependency of the Gibbs potential for a perfect gas. At constant temperature we have

\begin{equation*} dG_m(T,p) = V_m dp \quad \mbox{i.e.}\quad G_m^{ideal}(T,p) = G_m^{ideal}(T,p_0) + \int_{p_0}^p V_m dp = G_m^{ideal}(T,p_0) + R\, T \ln \frac{p}{p_0} \label{eq:Gmideal} \end{equation*}

(3.78)

For a real gas/fluid we just assume the same functionality but replace the pressure by the fugacity, i.e.

\begin{equation*} G_m(T,p) = G_m(T,p_0) + \int_{p_0}^p V_m dp = G_m^{ideal}(T,p_0) + R\, T \ln \frac{f}{f_0} = G_m^{ideal}(T,p_0) + R\, T \ln \frac{p}{p_0} + R\, T \ln \gamma \label{eq:Gmreal} \end{equation*}

(3.79)

Figure 3.10: Gibbs potential for a perfect and a real gas.

For the last equality we have used the definition of a fugacity coefficient \(\gamma = f / p\). One chooses standard condition \(p_0\) for which (all) real systems behave ideally, so for \(p \rightarrow p_0\)

\begin{equation*} G_m(T,p_0) = G_m^{ideal}(T,p_0) \quad \mbox{and} \quad p_0 = f_0 \label{eq:at_p0} \end{equation*}

(3.80)

which allows to write the residual Gibbs potential as

\begin{equation*} \begin{split} G_m^{res}(T,p) = &\;\; G_m(T,p) - G_m^{ideal}(T,p) = R\, T \, \ln \frac{f}{p} = R\, T \, \ln \gamma \\ = &\;\; \int_0^p \left( V_m - \frac{R\, T}{p} \right) dp \end{split} \label{eq:Gres_fugacity} \end{equation*}

(3.81)

i.e.

\begin{equation*} \begin{split} \gamma = &\;\; \exp \left(\frac{1}{RT} \int_0^p \left( V_m - \frac{R\, T}{p} \right) dp \right) \quad \mbox{with} \quad V_m = \frac{Z\,R\,T}{p} \\ \Rightarrow \; \gamma = &\;\; \exp \left( \int_0^p \frac{Z - 1}{p} dp \right) \end{split} \label{eq:gamma} \end{equation*}

(3.82)

so the fugacity (coefficient) is directly related to the compression factor \(Z = 1 + B' p + C' p^2 + \cdots\). Fig. 3.10 summarizes the results:

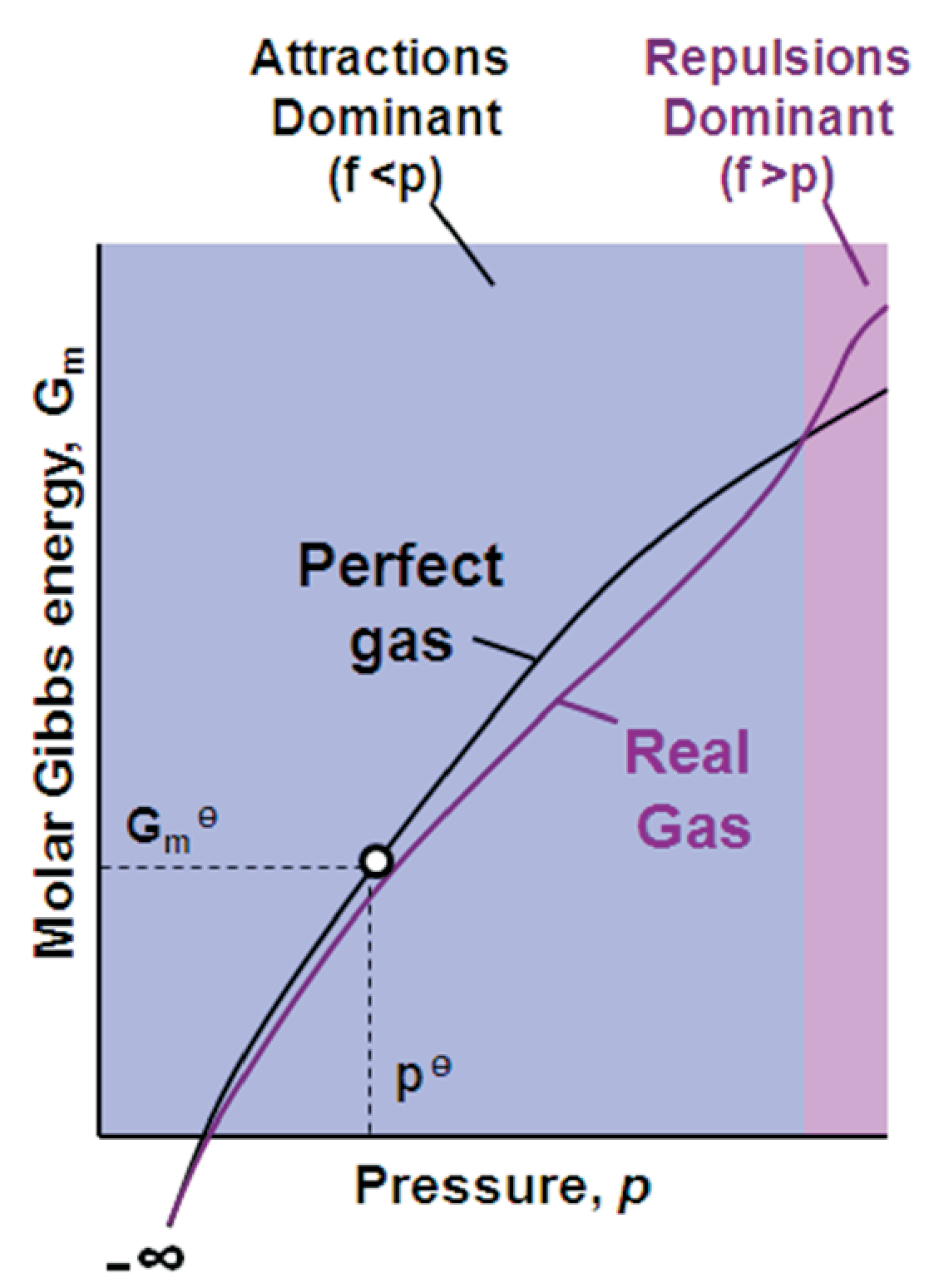
For \(p \rightarrow 0\) a real gas has the same \(G\) as a perfect gas, both states coincide.
For intermediate \(p\), the attractive forces are dominant, resulting in less escaping power, i.e. \(f \lt p\) and \(Z \lt 1\).
At high \(p\), the repulsive forces are dominant, leading to more escaping power, i.e. \(f \gt p\) and \(Z \gt 1\).

As an example for fugacity values the following table shows the experimental results for N\(_2\) at 273 K:


\(p\) / atm	1	10	100	1000

\(f\) / atm	0.99955	9.9560	97.03	1839