The pn-junction

5.7 The pn-junction

The concept

Following the concepts for the evaluation of the Boltzmann equation we analyze the undisturbed system purely quantum mechanically, i.e. we assume that the band structure (band gap, density of states, effective masses, ... ) is not changed by the perturbation.
The perturbation itself (here: the deviation of the lattice periodic potential by applying an external potential) will be describes purely classically.
Since the electrons are charged particles, they ”feel” this additional external electrical potential by band bending.
The non equilibrium thermodynamic state is described by quasi Fermi potentials.
Currents are described by gradients in the quasi Fermi potentials.

The equations
For a systematic description we define the (electrical) potentials

\begin{equation*} \psi:=-\frac{E_i}{q} \quad \mbox{and} \quad \Phi:=-\frac{\mu^*}{q} \qquad . \end{equation*}

(5.44)

Now we can write the charge densities as

\begin{equation*} n = n_i \exp\left( \frac{q(\psi -\Phi_n)}{k T}\right) \quad \mbox{and} \quad p = n_i \exp\left( \frac{q(\Phi_p -\psi)}{k T}\right) \qquad . \end{equation*}

(5.45)

Correspondingly we get

\begin{equation*} \Phi_n = \psi - \frac{kT}{q} \ln\left(\frac{n}{n_i} \right) \quad \mbox{and} \quad \Phi_p = \psi + \frac{kT}{q} \ln\left(\frac{p}{n_i} \right) \qquad , \end{equation*}

(5.46)

i.e. it resembles the Nernst equation resp. the properties of an ideal classical gas.
The mass action law applies for non equilibrium too:

\begin{equation*} n p = n_i^2 \exp\left(\frac{q(\Phi_p - \Phi_n)}{k T}\right) \end{equation*}

(5.47)

and for the integral current (electrical + diffusion) we find

\begin{equation*} \begin{split} \vec{J}_n & = q \mu_n \left(n \vec{E} +\frac{k T}{q} \vec{\nabla} n \right) \\ & = q \mu_n n (-\vec{\nabla} \psi ) + q \mu_n \frac{k T}{q} \left[\frac{q n}{kT}\left(\vec{\nabla} \psi - \vec{\nabla} \Phi_n\right) \right] \\ & = - q \mu_n n \vec{\nabla} \Phi_n \end{split} \end{equation*}

(5.48)

and correspondingly

\begin{equation*} \vec{J}_p = - q \mu_p p \vec{\nabla} \Phi_p \qquad . \end{equation*}

(5.49)

For thermodynamic equilibrium holds

\begin{equation*} \Phi_n = \Phi_p = \Phi = const. \qquad , \end{equation*} (5.50)

i.e.

\begin{equation*} \vec{J}_n = \vec{J}_p = \vec{0} \qquad , \end{equation*} (5.51)
The larger the mobility and the charge density, the smaller is the gradient of the quasi Fermi potentials for the same current density
The perturbation is then comparably smaller

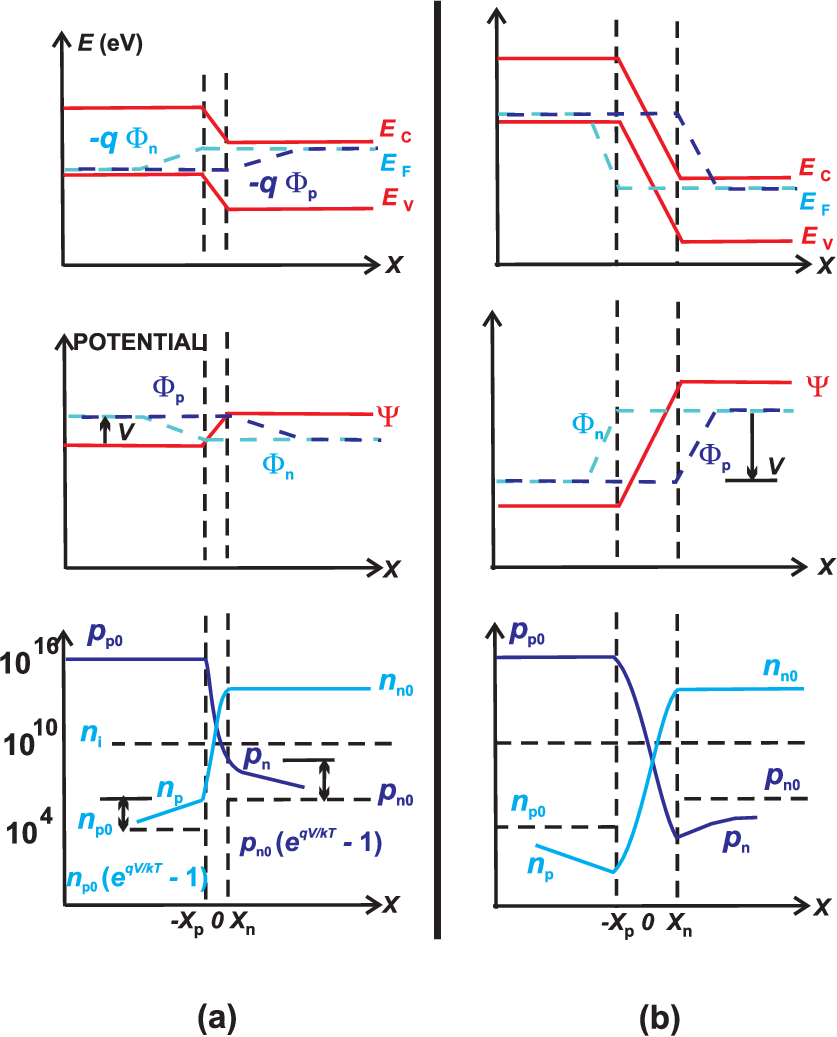
The following images illustrate the effect of current flow on the quasi-Fermi-energies in forward and reversed direction:

Energy band diagram: (a) forward direction (b) reversed direction.

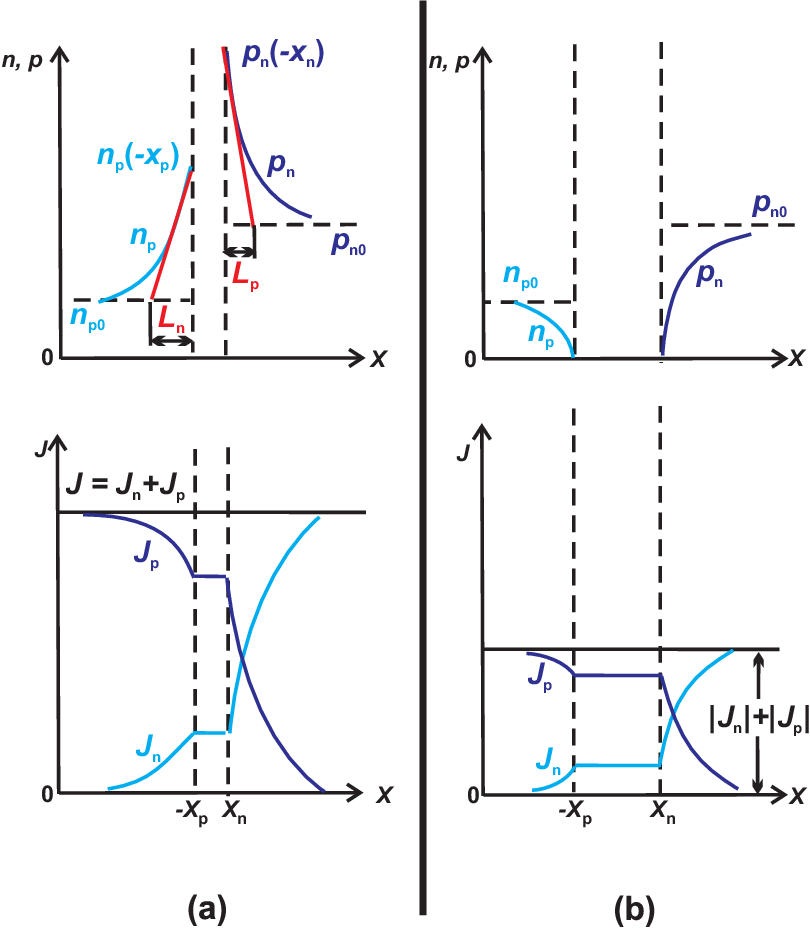
Carrier distribution and current densities (linear plots) for (a) forward biased condition and (b) reversed biased condition.

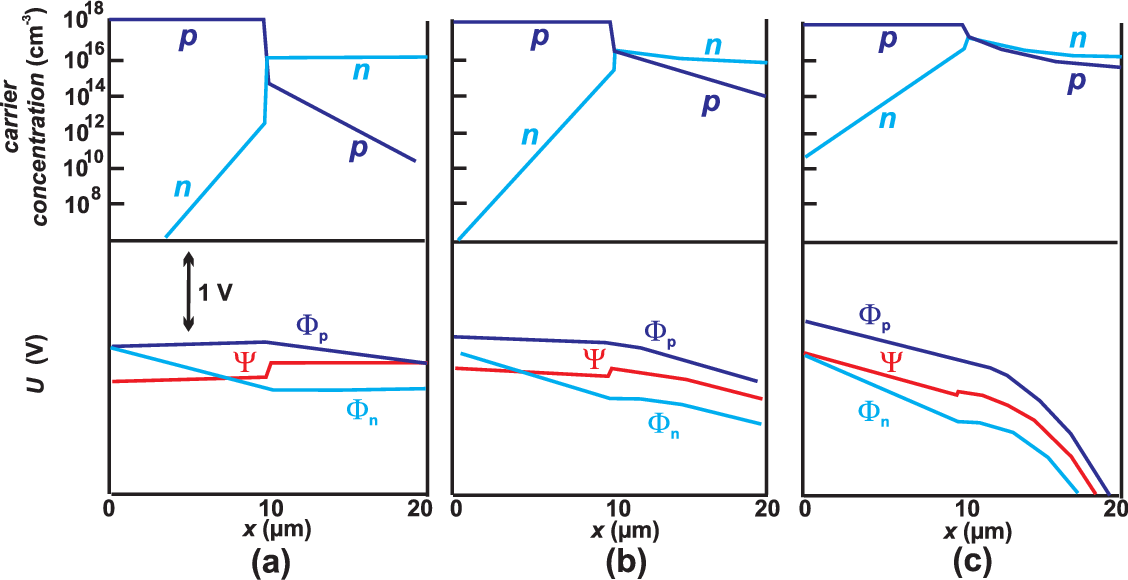
Carrier concentration and potentials for a pn junction operated at different current densities. (a) 10 A/cm\(^{2}\); (b) 10\(^{3}\) A/cm\(^{2}\); (c) 10\(^{4}\) A/cm\(^{2}\).