The semiconductor LASER

4.4 The semiconductor LASER

In a semiconductor LASER we do not have two single energy levels but two energy bands as LASER niveaus
Only light with \(h \nu \gt E_G\) can be absorbed in a semiconductor. So for the stimulated emission only this frequencies occur.
Let the rates for absorption, spontaneous and stimulated emission be

\begin{equation*} Z_{12}^{(abs)}\mbox{, }Z_{21}^{(spot)}\mbox{, and } Z_{21}^{(ind)} \end{equation*} (4.23)
Some additional background information you can find in the semiconductor script.

Transitions occur only from occupied states into unoccupied states. We therefor find

\begin{equation*} \begin{split} Z_{12}^{(abs)} & = K f(E_1)(1-f(E_2)) \varrho(\omega) \\ Z_{21}^{(ind)} & = K f(E_2)(1-f(E_1)) \varrho(\omega) \end{split} \end{equation*}

(4.24)

We find the same proportionality factor \(K\) for both processes since they are induced by quantum mechanics. (It is the same reason why \(B_{12} = B_{21}\) holds).
In case of LASERing the spontaneous emission can always be neglected in comparison to the induced emission. Light amplification of a frequency \(\omega\) therefor only occurs if

\begin{equation*} Z_{21}^{(ind)} \gt Z_{12}^{(abs)} \qquad . \end{equation*}

(4.25)

As LASER condition we find consequently

\begin{equation*} f(E_2)(1-f(E_1)) \gt f(E_1)(1-f(E_2)) \qquad . \end{equation*}

(4.26)

In thermodynamic equilibrium always holds

\begin{equation*} f(E_2) \ll f(E_1) \mbox{ and } (1-f(E_1)) \ll (1-f(E_2)) \qquad . \end{equation*}

(4.27)

The LASER in action therefor describes a state of extreme non equilibrium.
Description of non equilibrium in a semiconductor
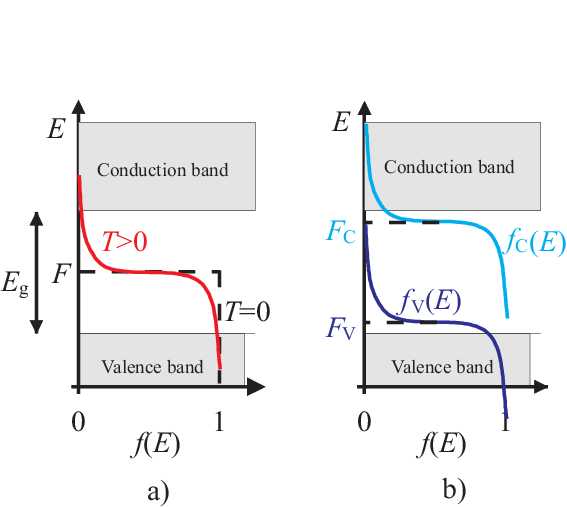
The thermodynamic equilibrium in a semiconductor is described by the Fermi energy and the temperature dependent shape of the Fermi statistics:

all electrons in all band are in thermal equilibrium
the relative occupation probabilities depend only on the energy differences in the grand canonical ensemble
the time which is necessary to reach the equilibrium depends on the slowest process
the slowest process has the smallest interaction probability

Excitation times:

Atomic transitions:	\(10^{-15} - 10^{-18} s\)
Intra band transitions:	\(10^{-8} - 10^{-12} s\)
Band-band transitions:	\(10^{-3} - 10^{-7} s\)

\(\Rightarrow\) after a time of ca. \(10^{-8} s\) the occupation probabilities of electrons within a band follow the Fermi statistics.

For one band the chemical potential exists which defines the electron number in this band
Different bands are not in thermal equilibrium
For different bands we need different chemical potentials
Electrons in different bands are handled as distinguishable particles
As for chemical reactions each type of particles has its own chemical potential
The interaction between distinguishable particles is explicitly written as reaction equations
In out case we explicitly name the band-band interactions to describe non equilibrium states

The Fermi statistics for the conduction band is

\begin{equation*} f_C(E) = \frac{1}{\exp\left(\frac{E-F_C}{k T}\right)+1} \end{equation*}

(4.28)

For the valence band we find

\begin{equation*} f_V(E) = \frac{1}{\exp\left(\frac{E-F_V}{k T}\right)+1} \end{equation*}

(4.29)

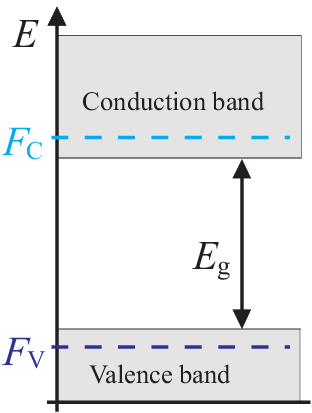
For the LASER condition we get

\begin{equation*} f_C(E_2)(1-f_V(E_1)) \gt f_V(E_1)(1-f_C(E_2)) \qquad , \end{equation*}

(4.30)

i.e.

\begin{equation*} \frac{1}{\exp\left(\frac{E_2-F_C}{k T}\right)+1} \frac{\exp\left(\frac{E_1-F_V}{k T}\right)}{\exp\left(\frac{E_1-F_V}{k T}\right)+1} \gt \frac{1}{\exp\left(\frac{E_1-F_V}{k T}\right)+1} \frac{\exp\left(\frac{E_2-F_C}{k T}\right)}{\exp\left(\frac{E_2-F_C}{k T}\right)+1} \qquad . \end{equation*}

(4.31)

This is equivalent to

\begin{equation*} F_C - F_V \gt E_2 - E_1 \geq E_G \qquad . \end{equation*}

(4.32)