The spectral density of radiation
We will discuss the electromagnetic
radiation coming out of a black radiator:
For photons the dispersion relation holds:
|
| \begin{equation*} \omega = c k \end{equation*} | (4.1) |
with \(c\): velocity of light.
Just as for the Debye model
we find
|
| \begin{equation*} N(k)=2 \left(\frac{L}{2 \pi}\right)^3 \frac{4}{3} \pi k^3 \end{equation*} | (4.2) |
The factor 2 sums up both planes for transverse electromagnetic waves. Again we get
|
| \begin{equation*} D(\omega)=\left(\frac{Vk^2}{\pi^2}\right) \frac{dk}{d\omega}=\frac{V\omega^2}{\pi^2c^3} \qquad , \end{equation*} | (4.3) |
and consequently the spatial spectral density of radiation
|
| \begin{equation*} \rho(\omega,T)=\frac{\omega^2}{\pi^2 c^3} \frac{\hbar \omega}{\exp\left(\frac{\hbar \omega}{k T}\right)-1} \qquad . \end{equation*} | (4.4) |
This is the famous radiation law of Max Planck.
Planck’s radiation
law as a balance between absorption and emission
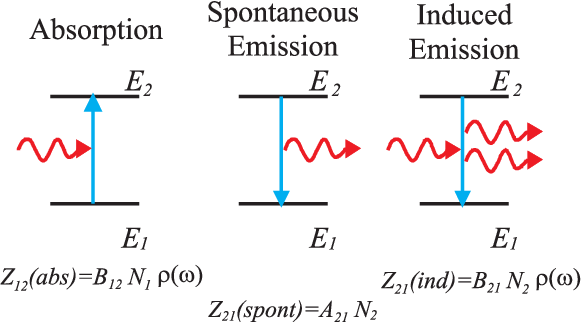
What kinds of radiation interaction exist between
two energy levels \(E_1\) and \(E_2\)?

The rate of absorption processes per time is proportional to the number \(N_1\) of atoms in the ground state and the energy density \(\varrho(\omega)\) of the electromagnetic field at the energy \(\omega\) is
|
| \begin{equation*} Z_{12}^{(abs)}=B_{12}N_1 \varrho(\omega) \qquad . \end{equation*} | (4.5) |
\(B_{12}\) is called the Einstein coefficient for absorption. This equation holds not only for thermodynamic equilibrium; therefor the parameter \(T\) was omitted.
The number of spontaneous emission processes per time is proportional to the number \(N_2\) of atoms in an excited state
|
| \begin{equation*} Z_{21}^{(spont)}=A_{21}N_2 \qquad . \end{equation*} | (4.6) |
If this process is dominant, we find
|
| \begin{equation*} Z_{21}^{(spont)}=-\frac{dN_2}{dt} \qquad , \end{equation*} | (4.7) |
i.e.
|
| \begin{equation*} \frac{dN_2}{dt}=-A_{21} N_2 \qquad , \end{equation*} | (4.8) |
with the solution
|
| \begin{equation*} N_2(t)=N_2(0)\exp\left(-A_{21} t \right) =N_2(0) \exp\left(- \frac{t}{\tau} \right) \qquad , \end{equation*} | (4.9) |
i.e. the excited atoms relax exponentially with a mean lifetime \(\tau\) defined by
|
| \begin{equation*} A_{21} = \frac{1}{\tau} \qquad . \end{equation*} | (4.10) |
\(A_{12}\) is called spontaneous transition probability.
\(\tau\) is called relaxation time. It quantifies how fast a system reaches again equilibrium after a perturbation.
Under the influence of radiation we find ”induced” transitions. The number of transitions per time interval is proportional to the number \(N_2\) of excited atoms and the energy density \(\varrho(\omega)\) of the radiation
|
| \begin{equation*} Z_{21}^{(ind)}=B_{21}N_2 \varrho(\omega) \qquad . \end{equation*} | (4.11) |
\(B_{21}\) is called Einstein coefficient of ”induced” (”stimulated”) emission.
For steady state (constant occupation numbers \(N_1\) and \(N_2\)) the following relation must hold:
|
| \begin{equation*} Z_{12}^{(abs)} = Z_{21}^{(spont)} + Z_{21}^{(ind)} \qquad , \end{equation*} | (4.12) |
i.e.
|
| \begin{equation*} B_{12} N_1 \varrho(\omega)=A_{21}N_2 + B_{21} N_2 \varrho(\omega) \qquad , \end{equation*} | (4.13) |
and consequently
|
| \begin{equation*} \varrho(\omega)= \frac{A_{21}}{\frac{N_1}{N_2}B_{12}- B_{21}} =\frac{\frac{A_{21}}{B_{21}}}{\frac{N_1}{N_2}\frac{B_{12}}{B_{21}}-1} \qquad . \end{equation*} | (4.14) |
For thermodynamic equilibrium at a temperature \(T\) we find:
(canonical ensemble)
|
| \begin{equation*} \frac{N_1}{N_2} =\exp\left(\frac{\epsilon_2-\epsilon_1}{kT}\right) = \exp\left(\frac{\hbar \omega}{kT}\right) \qquad . \end{equation*} | (4.15) |
leading to
|
| \begin{equation*} \varrho(\omega, T)= \frac{\frac{A_{21}}{B_{21}}}{\frac{B_{12}}{B_{21}} \exp\left(\frac{\hbar \omega}{kT}\right) - 1} \qquad . \end{equation*} | (4.16) |
Comparing with the Bose statistics we find:
|
| \begin{equation*} A_{21} = \frac{\hbar \omega^3}{\pi^2 c^3} B_{21} \qquad , \end{equation*} | (4.17) |
and
|
| \begin{equation*} B_{12} = B_{21} \qquad . \end{equation*} | (4.18) |
The above discussion is not a deduction of the Bose statistics but an interpretation of the underlying processes.
Essential for the interpretation are not only the spontaneous emission and absorption but also the stimulated emission.
These three processes are not restricted to phonons and black body radiator but belong to Bosons in general.
Non equilibrium phenomena are described as well by these processes.
The spontaneous emission leads to a random photon radiation. Therefor no phase coupling exists between the photons.
The induced emission generates light with exactly the same phase as the incoming light. We get a coherent light beam (in time and in space, interference’s are possible, light is parallel,...)
LASER light origins from this induced emission process!
© J. Carstensen (Stat. Meth.)