Specific heat capacitance of phonons (Bosons)

3.4 Specific heat capacitance of phonons (Bosons)

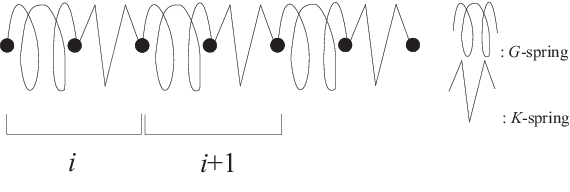
One-dimensional lattice vibrations
We investigate a chain of identical atoms which are coupled by different kinds of springs:

Always two atoms form a unit (basis) addressed by an index \(i\).
The lattice distance shall be \(a\).
The excursion of both atoms is denominated by \(u_1\) and \(u_2\):
for the potential energy we find:

\begin{equation*} U^{harm} = \frac{K}{2}\sum_n \left[u_1(na)-u_2(na)\right]^2 + \frac{G}{2}\sum_n \left[u_2(na)-u_1((n+1)a)\right]^2 \qquad . \end{equation*}

(3.19)

The equations of motion are:

\begin{equation*} \begin{split} M\ddot{u}_1(na) & = -\frac{\partial U^{harm}}{\partial u_1(na)} \\ & = -K[u_1(na)-u_2(na)]-G[u_1(na)-u_2((n-1)a)] \label{motion1} \end{split} \end{equation*}

(3.20)

\begin{equation*} \begin{split} M\ddot{u}_2(na) & = -\frac{\partial U^{harm}}{\partial u_2(na)} \\ & = -K[u_2(na)-u_1(na)]-G[u_2(na)-u_1((n+1)a)] \label{motion2} \end{split} \end{equation*}

(3.21)

Due to the translational invariance we search for lattice periodic functions. Just for simplicity we use periodic boundary conditions:

\begin{equation*} \begin{split} u_1(na) & = \epsilon_1 \exp\left(i(k n a-\omega t)\right)\\ u_2(na) & = \epsilon_2 \exp\left(i(k n a-\omega t)\right) \end{split} \end{equation*}

(3.22)

\(\epsilon_1\) and \(\epsilon_2\) are parameters which describe the relative amplitudes and phases between both atoms.
For \(k\) the following relation holds:

\begin{equation*} \exp(ikNa) = 1\; \mbox{, i.e.} \quad k = \frac{2 \pi}{a} \frac{n}{N}, \qquad n = -\frac{N}{2}, .... , \frac{N}{2} \quad . \end{equation*}

(3.23)

Including this into Eq. (3.20) and Eq. (3.21) we get:

\begin{equation*} \begin{split} [M \omega^2-(K+G)]\epsilon_1 + (K+G e^{-i k a}) \epsilon_2 & = 0 \\ (K+G e^{-i k a}) \epsilon_1 + [M \omega^2-(K+G)] \epsilon_2 & = 0 \end{split} \end{equation*}

(3.24)

This system of linear equations only has solutions if the coefficient determinant vanishes:

\begin{equation*} [M \omega^2-(K+G)]^2 = \left|K+G e^{-i k a}\right|^2=K^2+G^2+2KG \cos(ka) \qquad . \end{equation*}

(3.25)

We find

\begin{equation*} \omega^2(k) = \frac{K+G}{M}\pm\frac{1}{M}\sqrt{K^2+G^2+2KG \cos(ka)} \end{equation*}

(3.26)

and

\begin{equation*} \frac{\epsilon_2}{\epsilon_1} = \mp \frac{K+G e^{i k a}}{\left|K+G e^{i k a}\right|} \qquad . \end{equation*}

(3.27)

For the \(N\) different \(k\)-values we always find two \(\omega\)-values, i.e. we find \(2N\) modes; this corresponds to the \(2N\) degrees of freedom (2 atoms in \(N\) elementary cells).
We can choose

\begin{equation*} K \gt G \qquad . \end{equation*}

(3.28)

The both solutions are:
1)

\begin{equation*} \omega(0) = \sqrt{2 \frac{K+G}{M}} \;\mbox{, and} \quad \frac{\epsilon_2}{\epsilon_1} \lt 0 \quad , \end{equation*}

(3.29)

i.e. both atoms oscillate in anti-phase. If the atoms are charged, thus a dipole moment would be introduced. Light can couple at this oscillations. Therefor the solution is called the optical mode.
2) We find

\begin{equation*} \omega(0) = 0 \;\mbox{, and} \quad \frac{\epsilon_2}{\epsilon_1} \gt 0 \quad , \end{equation*}

(3.30)

i.e. both atoms oscillate in phase. We will find density oscillations within the crystal. A sound wave will move through the crystal. Therefor his solution is called the acoustic mode.