 |
First we get a few important relations and numbers. |
|
 |
If 1/kT = 40 eV–1 at 300 K, we have 1/kT
= 40 · 300/400 = 30 eV–1 at 400 K |
|
|
The current densities j1 and j2
can always be written as |
| |
| j1 | =
| c1 · ni 2 |
= |
j1' · exp–(Eg/kT) |
| | |
| |
| | j2 |
= |
c2 · ni |
= |
j2' · exp–(Eg/2kT) |
|
| j1' | =
| j1 · exp(Eg/kT) |
| | |
|
| j2' | = |
j2 · exp(Eg/2kT) |
|
|
|
This gives us the following numbers: |
| |
| |
Theory |
Measured |
| |
j1 |
j2 |
j1 |
j2 |
| Calculated ji' |
2.06 · 105 A/cm2 |
5.74 · 10–1 A/cm2 |
1.29 · 1010 A/cm2 |
3.58 · 102 A/cm2 |
| |
T
= 300 K |
Starting values ji
U = 0 V |
1.6 · 10–14 A/cm2 |
1.6 · 10–10 A/cm2 |
10–9 A/cm2 |
10–7 A/cm2 |
Calculated ji
U = 0.5
|
7.76 · 10–6 A/cm2 |
3.52 · 10–7 A/cm2 |
0.46 A/cm2 |
2.2 · 10–3 A/cm2 |
| |
T
= 400 K |
Starting values ji
U = 0 V |
9.60 · 10–10 A/cm2 |
3.92 · 10–8 A/cm2 |
6.01 · 10–5 A/cm2 |
2,44 · 10–5 A/cm2 |
Calculated ji
U = 0,5 V |
9.67 · 10–3 A/cm2 |
1,5 · 10–4 A/cm2 |
|
|
| |
|
|
|
|
|
|
Now to the questions:
Question 1. Construct rather quantitatively the logarithmic IV characteristics (= log j -
eU plot) of two solar cells with the j2 and j2 values as given
in the table.
Question 2: Determine the open circuit voltage UOC for room temperature and for 400 K
and discuss your finding. |
| |
|
|
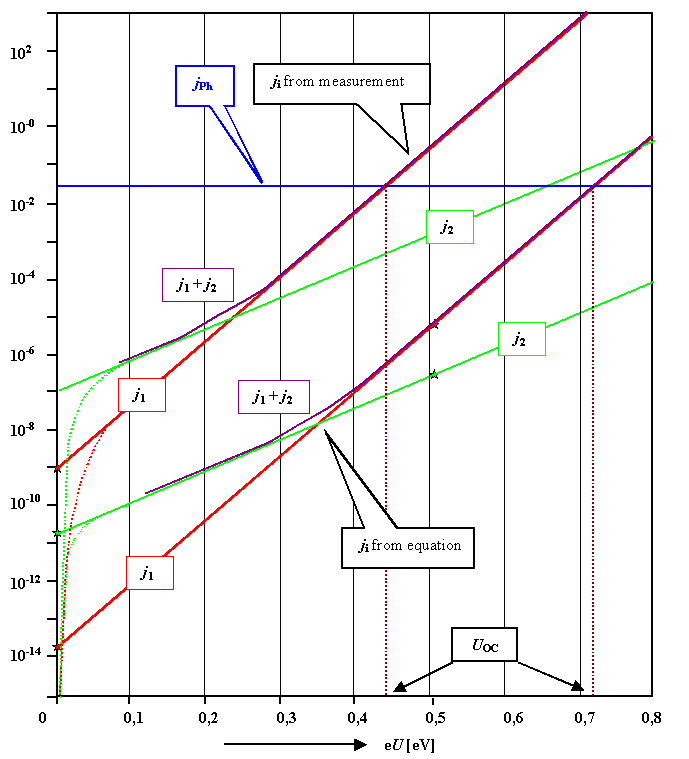
Constructing the graph is easy now; here is the result: |
| |
|
|
|
We note that the "-1" term can be neglected as soon as we have
current density values about 10 times larger then the starting values, i.e. below U
» 0.1 V. At lower values this term dominates the characteristics by forcing the currents
to zero, i.e. to –¥ in a log plot, but that is of no interest here. |
|
|
The addition of both curves only introduces a slight "rounding" at
the intersection point. |
|
|
The open circuit voltage follows from the intersection of the j(U)
curves with a straight line at j = – jPh. It is immediately clear that only the j1
part is of interest here. |
|
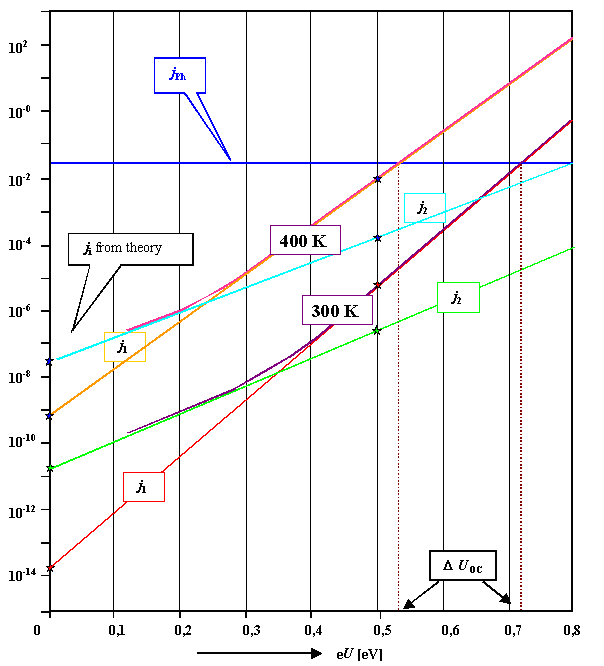
The effect of temperature is shown in a separate graph and only for the "theoretical"
set of the jPh: |
|
|
|
|
|
While the decreasing slope of the curves would increase UOC,
the large increase in the starting value of j1 has a much stronger effect and causes a substantial
decrease of UOC with temperature. |
| |
| |
© H. Föll (Semiconductor Technology - Script)
With frame
Basic IU-Characteristics of Solar Cells