Solution to Exercise 8.1-1

Exponential Growth

1. The output of the solar cell industry in 2006 - 2008 grew by 40 % per year. Let's assume that all solar cells installed in 2007 produced a total energy of 0.1 GW /year. Calculate (and plot) the installed power as a function of time up to 2050 for growth rates of a' = 20 %, 30 %, 40 %, and 50 %. What is the proper equation?
The general equation is P(t) = P0 · exp(a · t) and we know P(t = 0 a) = 100 MW and P(t = 1a) = 100 MW + (a'/100) · 100 MW; a' is the given growth rate in %
It follows that
P(t = 1a)  =  100 MW · exp(a · 1a · a–1)
     
   =  100 MW + (a'/100) · 100 MW
     
a  =  ln(1 + a'/100) a–1
     
   =  (0.182; 0.262; 0.336; 0.405) a–1
for growth rates of
20% ; 30%; 40%; 50%
 
2. Calculate (and plot) the installed power as a function of time up to 2050 for growth rates of 20 %, 30 %, 40 %, and 50 %.
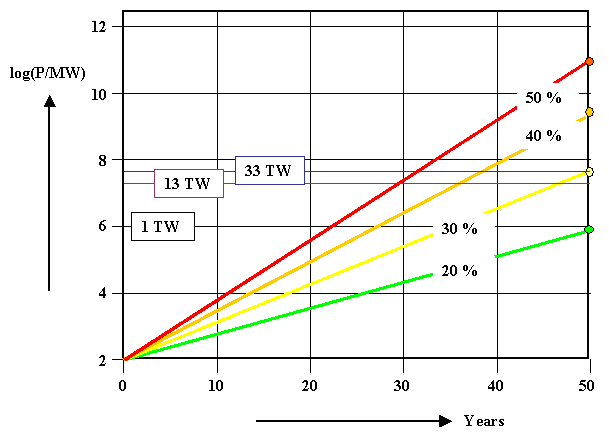
That's easy and we do it, of course, in a log P(t) plot. What we get looks like this:
Exponential growth of solar power
 
3. What follows form the results with respect to the world-wide power scenario as described in the link??
It follows that with the present growth rate of 40 % all of the world's energy demands can be produced by solar cells in 35 - 38 years - be it the present 13 TW or the predicted 33 TW
That looks like a "Milchmädchenrechnung" (i.e. very naive), because that's what it is. If we can sustain a growth rate of 40 % for 30 - 40 years remains to be seen. It's unlikely, but not impossible. The semiconductor industry, for example, sustained a growth rate of about 30 % by now for more than 35 years, and no end is in sight.
     
4. Plot the demand for Si, assuming that a standard (1000 x 1000 x 0.1) mm3 Si solar cell generates 10 W on average. Will there be enough Si? How do the amounts of Si needed compare to other essential raw materials?
The volume is 105 mm3 = 100 cm2. With a density of 2.33 g/cm3 we have 23.2 g/W.
The present (2007) production of (solar grade) Si per year is roughly 20.000 to = 2 · 1010 g; corresponding to 862 MW. If we want to produce 1 TW, we would need 23.2 · 1013 g = 23.2 · 107 to of Si.
That looks like a lot of Si. Yes, but look at the present world production of:
  • Iron / Steel: » 780 · 106 to.
  • Coal: » 5 000 · 106 to.
  • Al » 22 · 106 to.
So a few million tons of Si is definitely within present day capabilities
 

With frame With frame as PDF

go to Joules, Watts and kWhrs

go to Exercise Basic 8.1-1

© H. Föll (Semiconductor Technology - Script)