 |
We want to show that the following two equations are equivalent for equilibrium: |
|
|
| nep(U ) |
÷
÷ |
SCR
edge | = |
nen (U) |
÷
÷ |
SCR
edge |
· exp – |
e(Vn + U)
kT |
| n e p(U = 0) | =
| ni2
nhp (U = 0) |
|
|
|
 |
The first equation then simplifies to |
| |
| nep(U) |
÷
÷ |
SCR
edge | = |
nen(U) |
÷
÷ |
SCR
edge |
· exp – | eVn
kT | = |
nen(U ) |
÷
÷ |
SCR
edge |
· exp – |
DEF
kT |
|
|
| |
 |
Start with the equation for the majority carrier concentration nhp(U
= 0) in general and the definitions of the energies: |
|
|
| nhp(U = 0) |
= Neff p · exp – |
EF – EV p
kT |
| e·Vn | = |
Difference of
band edges | = |
EVp – EVn = ECp
– ECn = D E
F |
|
|
|
 |
Consult the solution to the Poisson equation
if you are unsure (the relevant diagram is reprinted below) and recall that in the band diagram, the energy scale refers to electrons, which carry a negative electric charge –
so that the electrostatic potential contributes with a negative sign. |
|
 |
Also note that EF
, of course, is constant in equilibrium, and DEF
thus refers to the difference in Fermi energies before the contact ! |
| |
|
 |
E
Vp thus can be expressed as EV
p = EVn + DEF . |
|
 |
This brings you already to the n-side. However, you want to find nen
in the equation, and for that you need a factor ECn – EF.
|
|
 |
So, express EV n in terms of E
Cn via EV n = ECn – Eg
with Eg = band gap. This yields |
|
|
| nhp(U = 0) |
= Neff p · exp – |
EF – ECn + Eg – D
EF
kT |
|
|
 |
You now have terms that occur in the definition of the electron density in n-Si
[namely, EF – EC n = – (EC
n – EF)] and for the intrinsic carrier density (namely, Eg).
|
|
 |
So, multiply with Neff n / Neff
n, remember that ni2 = Neffp · Neffn
· exp – Eg/(kT), and 1/nen = 1/N effn
· exp[(E Cn – EF)/(k T)]; thus, you have |
| |
| nhp(U = 0) | =
| ni2
nen |
· exp |
DEF
kT |
|
|
 |
This gives for nen: |
| |
| nen(U = 0) | =
| ni2
nhp
| · exp |
D EF
kT |
|
|
|
 |
We now can substitute nen in our first
equation and obtain |
| |
| ne p |
÷
÷
÷ | SCR
edge |
= | n i2
nhp | · exp |
DEF
kT |
· exp – |
DEF
kT |
|
|
 |
That is exactly the second equation – Q.E.D. |
© H. Föll (Semiconductors - Script)
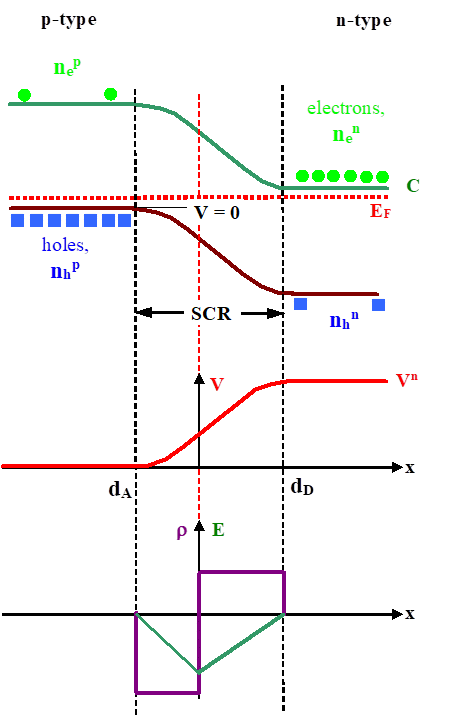
![]() Solving the Poisson Equation for p-n-Junctions
Solving the Poisson Equation for p-n-Junctions