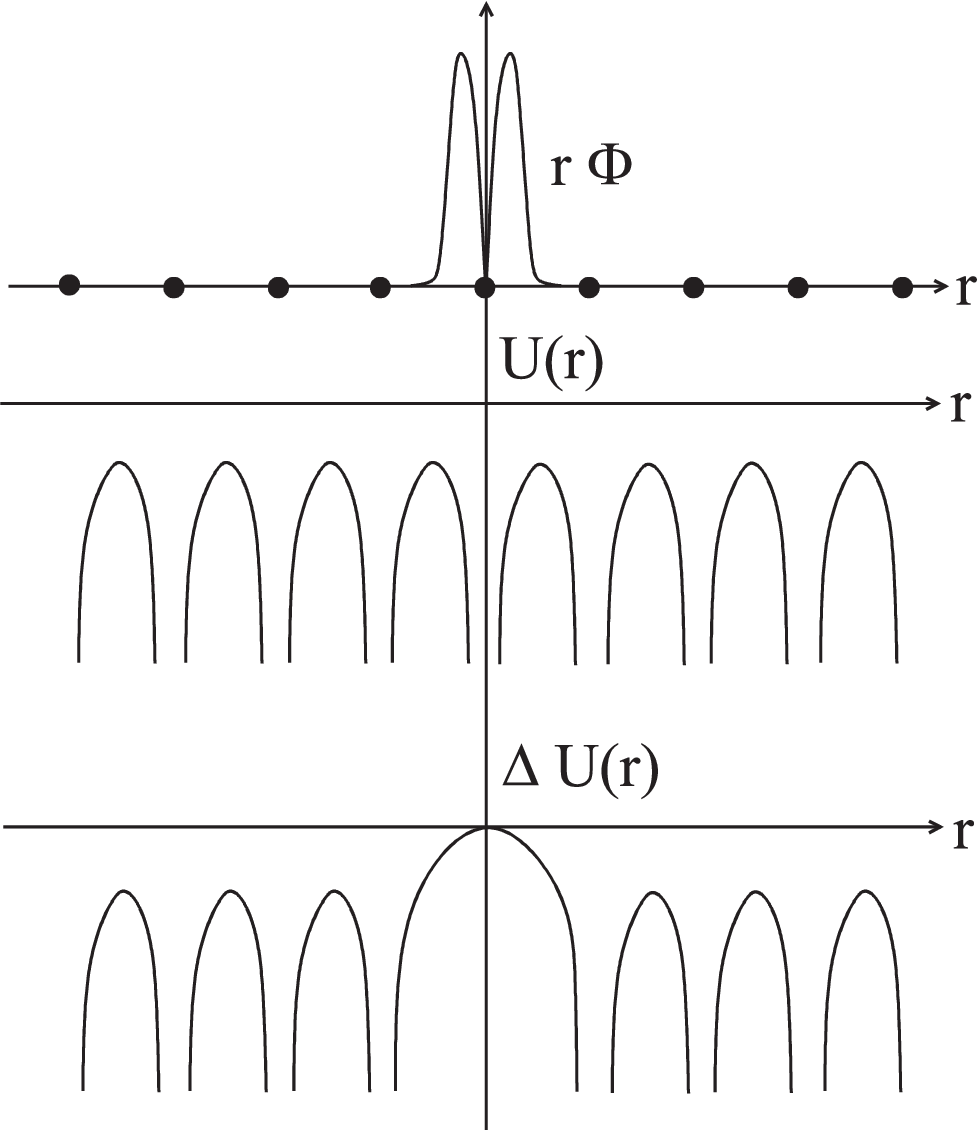
Fig. 4.1 Along a series of atom positions the range of the atomic
wave functions \(\Phi\), the periodic lattice potential \(U(r)\) and the perturbation of the atomic
wave unction \(\Delta U(r)\) is plotted.
Even the perfect crystal can not be calculated exactly since
the Hamiltonian is not known exactly
the Eigenvalues of a known Hamiltonian can not be calculated exactly
the correlation’s between electrons often break the symmetry of the system
Therefore we will discuss two approximations which describe two limits of a solid.
Expanding into plane waves
The Eigenvectors of free particles are plane waves. Describing a solid not taking into
account the periodic lattice potential, we reach the model of a free electron gas:
|
| \begin{equation*} \psi_{nk}(\vec{r}) = e^{i \vec{k} \vec{r}} c_{nk} \qquad . \label{plane_w1} \end{equation*} | (4.27) |
Since all constants \(c_n\) obviously display the periodicity of the lattice,
the Bloch-Theorem (4.2) is fulfilled.
This approximation can be improved significantly by taking into account a perturbation of the periodic lattice. We substitute
Eq. (4.27) by
|
| \begin{equation*} \psi_{nk}(\vec{r}) = e^{i \vec{k} \vec{r}} c_{nk}(\vec{r}) \qquad . \label{plane_w2} \end{equation*} | (4.28) |
The functions \(c_{nk}(\vec{r})\) display the lattice periodicity and are constant on a defined set of intervals; they therefore obey the Bloch condition. This so-called Kronig-Penney model can explain several aspects, e.g.
the occurrence of band gaps at the Brillouin zones,
Bragg reflection at the Brillouin zones,
effective masses of electrons
energy bands by folding back the energy parable
This approach describes only these solids adequately which consist of almost free electrons.
These electrons show a great mobility and will not be scattered effectively by the lattice atoms. We precisely described
the properties of metal electrons (S-electrons) which exist e.g. in alkaline end earth-alkaline metals. The more
plane waves are used for the description of the solid (the more accurate we approximate the lattice potential) the better
we will describe the electronic state of these solids. The expansion into plane waves is quite simple on a computer. Taking
into account more expansion coefficients (increasing the computational time) one gets quite good results even for systems
for which the above requirements do not met optimally.
Expanding into atomic wave functions
Often plane waves are not at all a good approximation for the electronic states of
a solid:
| Ionic crystals | strong influence of the lattice potential |
| Insulators | no free electrons |
| Semiconductors | strong covalent bonds, atomic like orbitals |
Here we find a strong dominance of the atomic character of the electronic wave functions which defines the properties of the solid. Considering the bad conductivity of these solids is a strong hint that plane waves will not be an effective tool to approximate these solids:
bad electronic conductivity
\(\Rightarrow\) no free electrons
\(\Rightarrow\) no good description by plane waves
Therefore we will use an approximation which implements the lattice periodicity as a ”small” perturbation for the atomic orbitals.
CONCEPT:
The lattice periodic potential is described by the function
|
| \begin{equation*} U(r) = U(r + R) \end{equation*} | (4.29) |
We expand at every lattice point R into atomic wave
|
| \begin{equation*} H_{at}\psi_n = E_n \psi_n \label{hat} \end{equation*} | (4.30) |
These functions form for each point a CONS (Complete orthonormal system). To evaluate an arbitrary function one has to expand it in every point into the CONS. For a solid and using the above approximations we only have to expand the state function at the positions of atoms.
The periodicity of the crystal is implemented by the Bloch theorem:
|
| \begin{equation*} \psi(r + R)= e^{i k R}\psi(r) \end{equation*} | (4.31) |
All calculations can therefore be restricted to the first Brillouin zone.
The Hamiltonian for the first Brillouin zone (centered around the position of the atom \(R\)) can be written as
|
| \begin{equation*} H = H_{at} + \Delta U(r) \end{equation*} | (4.32) |
The kinetic energy is completely included in \(H_{at}\). \(\Delta
U(r)\) describes the additional influence of the neighboring atoms for the position \(R\).
The atomic wave functions have a range which follows the above assumptions (as displayed in Fig. 4.1). Thus they
do not overlap strongly with the orbitals of their neighboring atoms.
The complete wave function is
summed up using the atomic wave functions of Eq. (4.30):
|
| \begin{equation*} \psi_{nk}(r) = \sum_R e^{i k R} \Phi_n(r - R) \label{phase_sum} \end{equation*} | (4.33) |

Fig. 4.1 Along a series of atom positions the range of the atomic
wave functions \(\Phi\), the periodic lattice potential \(U(r)\) and the perturbation of the atomic
wave unction \(\Delta U(r)\) is plotted.
For this function the Bloch theorem holds:
If \(\Delta U(r) = 0\), Eq. (4.33) is the exact wave function of a solid.
In this case the solid would consist of isolated atoms.
All energy states would be the atomic orbitals \(E_n\) of Eq. (4.30).
To include the perturbation \(\Delta U(r)\) of the atomic energy levels we use in Eq. (4.33) the linear combination of atomic orbitals
|
| \begin{equation*} \Phi(r) = \sum_n b_n \psi_n(r) \label{sum_r_phi2} \end{equation*} | (4.35) |
Thus we replace the purely atomic states with mixed atomic states. The calculation of these coefficients \(b_n\) is the main task in the following.
© J. Carstensen (Quantum Mech.)