A Model for Current-Voltage Oscillations at the Silicon Electrode and
Comparison with Experimental Results

J. Carstensen, R. Prange and H. Föll

Faculty of Engineering

Kaiserstr. 2

24143 Kiel

Germany

Abstract

The first consistent and complete model of current oscillations at the Si-electrode is presented. The only basic assumption needed is an ionic break-through mechanism which is postulated to occur in thin oxides under oxidizing electrode conditions, leading to an enhanced and localized ion transport to the Si - SiO₂ interface. Choosing reasonable values for 3 corresponding physical parameters and using a Monte Carlo simulation technique, first-principle calculations yield quantitative data in excellent agreement with numerous experimental results, including the value of the current, the roughness of the surface, the average oxide thickness, and the capacitance as a function of the phase of oscillations. as well as the frequency of the oscillations as a function of applied voltage, current density, etching rate or HF-concentration, and temperature.

Introduction

The reactive solid-liquid contact is not too well understood in general, and this is particularly true for the Si - liquid contact. Even the supposedly simple chemical etching of Si or SiO₂ is still full of surprises, as anyone employed in microelectronics will acknowledge. More specifically, a case could be made that the current-carrying solid-liquid contact, with Si as the electrode and an electrolyte containing some F^--Ions- commonly in the form of diluted HF - is not understood at all. Nobody can predict the complex features of the current-carrying Si-HF contact; not even the voltage-current characteristics obtained in simple experiments are computable from first principles. Porous Silicon, with an increasing wealth of features that are mostly not understood [1, 2], and the totally mystifying, current-voltage oscillations that occur in a large region of the available parameter space [2, 3, 4], bear witness to this claim.

This paper deals exclusively with voltage-current oscillations in Si, but it is worthwhile to point out that this phenomenon is not specific to the Si electrode. In fact, it was Faraday some 100 years ago, who already remarked on oscillating electrodes (a term we will use for both current- or voltage oscillations depending on the experimental conditions chosen) [5], but until now no general model has been developed. The recent interest in the Si electrochemistry, triggered by the observation that one kind of porous Si shows strong luminescence [6, 7], has also spurred a number of investigations on the current-voltage oscillations observed under special, but easily established conditions in Si [8, 9, 10, 11, 12, 13, 14]. It is now generally accepted that oscillations can occur under conditions where an oxide is formed by the current and is in turn dissolved by the electrolyte. However, despite these recent efforts, not one single consistent model of electrode oscillations has been suggested so far [15].

Any model of an oscillating electrode needs three ingredients: Firstly, a mechanism for a local oscillator is required. This is obvious, because without an atomic-scale oscillation mechanism, no oscillations can occur. More specifically, a mechanism that describes some non-linear behavior of the electrode on an atomic scale must exist, because linear relations, e.g. the linear interplay of oxide formation proportional to the current and chemical oxide dissolution, will not lead to stable oscillations but to a steady-state equilibrium, as already pointed out by Frank in 1978 [16].

Still obvious, after some deliberation, is the second ingredient: A synchronization mechanism that forces at least some of the local oscillators to synchronize, is a must for "macroscopic" electrode oscillations, i.e. oscillations observed with specimens of macroscopic dimensions. Local current oscillators that are not synchronized to some extent, will, if summed up to yield the total current, just lead to an average current that shows no oscillation but at best some "colored" noise.

Less obvious is the third and last ingredient needed for any complete model of an oscillating electrode. Perhaps surprisingly, a desynchronization mechanism is needed just as well. This is so because otherwise electrodes would either oscillate strongly or not at all. Many phenomena that are observed (e.g. damped oscillations [17]) or predicted (e.g. non-synchronized oscillations that manifest themselves in "colored" noise) would not be possible without a mechanism that opposes synchronization.

In this paper a complete model of the oscillating Si electrode under "low frequency" conditions is presented for the first time. "Low frequency" conditions, in a preliminary imprecise definition, are obtained for relatively low HF concentrations, voltages, or currents, respectively. The term will be precisely defined in what follows, but it is prudent to point out at this stage that the model presented does not yet include all kinds of observed electrode oscillations.

Fig. 1 illustrates a few of the experimental data that need to be modeled. The current density J(t) as a function of time t, the frequency f(U_an, J, C_HF,) of the oscillations as a function of the applied anodic voltage U_an, the current density J or the concentration of the electrolyte C_HF, needs to be calculated. But also less obvious parameters as, e.g., the average oxide thickness, the capacitance of the solid-liquid junction, or the roughness of the solid surface, should be obtained with a complete model.

The Model

We start with the generally accepted fact that the local mechanism of an oscillating Si-electrode relies on the formation and dissolution of SiO₂. Several experiments demonstrate that the resulting oxide layer is less than 10 nm thick - on an area and time average, see, e.g. [18, 19].

On this base we first postulate: All of the current flowing across the interface produces oxide at all times and in all places. This is the quantitative definition of the "low frequency" condition; it must not be true for all oscillations observed. It is possible - e.g. at higher currents and frequencies - that some part of the current does not produce oxide, but this will not concern us in this paper. It should be emphasized that this is not a strong assumptions and that it poses no limits on the spatial or time dependence of the current. Local current flow thus always increases the local thickness s of the oxide layer. The oxide thickness in turn may still depend on position as well as on time; s=s(x,y,t). The relation

(1)

with b being a geometrically determined parameter (essentially the valence of the process, i.e. the number of holes needed to produce one SiO₂ unit) and a the purely chemically determined dissolution rate), must hold locally and at all times. The dissolution rate, to be totally general, must not be a constant but could depend on local conditions. This would be the case, e.g., if the chemical dissolution rate depends on the field strength and therefore on the local thickness of the oxide, but also if the surface of the oxide is rough in some places but not in others.

O^- Ions must migrate through the existing oxide layer to be consumed at the interface. As already stressed by several authors [4, 20], the ion transport through the oxide layer holds the key for the understanding of the oscillation phenomenon. We propose in our only strong assumption that the strong electric field present across the (thin) oxide is a nonlinear driving force for the ion transport through the oxide. Since a uniform field-enhanced diffusion is not sufficiently nonlinear, we propose an "ionic breakthrough" mechanism. Whenever the electric field in the oxide approaches an upper critical value E_max, a break-through channel or pore is formed, leading to a highly localized ionic current J_ox to be matched by the hole current at the interface that is largely independent of the oxide thickness. At and around the pore tip the oxidation is enhanced, leading to a roughly semispherical oxide "inclusion" around the pore. Since SiO₂ formed from a given volume of Si almost doubles in volume, a corresponding bump will be formed on the oxide-electrolyte interface, i.e. the oxide surface. Fig. 2a illustrates this mechanism. Inherent in this mechanism is a lateral growth of oxide relative to the pore tip, resulting, e.g., from rapid diffusion of O^- ions in the SiO₂ - Si interface or from a movement of the channel end to the thin part of the oxide.

It is not important for the model exactly how the ionic break-through occurs or which mechanism establishes lateral oxide growth in which precise geometry. It is likely, e.g. that the ionic break-through is linked to or even triggered by a normal (avalanche) electronic break-through. But since this is of no importance for what follows, we will not discuss or speculate about the detailed mechanisms.

We will now specify our basic assumption in order to enable quantitative modeling. While the oxide thickness increases around the pore tip, the electric field decreases without reducing the ion transport through the oxide. At a minimum value E_min the oxide growth stops. This means that in analogy to an electronic breakthrough, we postulate that after starting the ion transport through the oxide, the electric field can be reduced significantly without reducing the ion current. Leaving aside a microscopic picture for the ion transport and only pointing out that the ions have to pass a 2 to 8 nm thick oxide layer, a mechanism emerges, centering around a narrow (nm or less) channel or pore through the oxide, which is opened at high field strength and closed at low field strength. With the local anodic potential U_an, and defining E_max as the maximal field strength needed for ionic breakthrough and E_min as the minimal field strength for the ending of the ionic current flow, the relations

and (2)

for the minimum and maximum oxide thickness s are obtained. The local oxide layer thickness thus increases by approximately

Ds=s_max - s_min, (3)

while the channel is "open".

This model reverses ideas presented before [2], where an electronic breakthrough, leading to a locally enhanced non-oxidizing current, was envisioned as the cause for electrode oscillations.

It is obvious that the ionic break through mechanism indeed provides for the required local oscillator. However, as stated above, it will not necessarily account for macroscopic oscillations that can only be observed when a large number of local oscillators are synchronized. This is true even for the case of a perfectly homogeneous electrode, where all local oscillators would start at the same time, because we have to make allowances for the statistical nature of the postulated break-through process. E_min and E_max must be seen as lower and upper limits for the ionic breakthrough (or "opening" and "closing") of the channels, and, in accounting for the statistical nature of these events, we have to define two functions W(E) and R(E) which give the probability for the opening and the closing of a channel within a time Dt on an area DA. These functions are detailed in the appendix.

The statistical nature of the proposed process, leave alone the more realistic situation where the oxide layer would never be totally homogeneous over large areas at any one time during an oscillation, would necessarily cause a rapid desynchronization of originally synchronized local oscillators. No macroscopic oscillations would be observed after some time, because the local currents are then summed up with random phases, yielding a constant, if noisy macroscopic current. We emphasize that a non-oscillating electrode in this model does not prove the absence of local oscillations, but may only show the absence of a synchronization mechanism. If one were to measure the spectral intensity of the current noise, we predict that in this case a strong peak would be present at the typical frequency of the local oscillators.

Our local oscillator, however, has a built-in synchronization mechanism with respect to its nearest neighbors. This results from the lateral growth of the oxide around the pore tip as illustrated in Fig. 2a-c. Let us assume that a new channel (No. 3 in Fig. 2b) is opened close to an active one (No. 2 in Fig. 2b). This neighboring channel then must produce less oxide before it stops again, because it is "helped" by the already active pore (cf. Fig. 2c). Its stopping-point is thus already much closer to the stopping-point of the first channel; we could say that its dynamics are enhanced until it catches up with the first oscillator. After a few cycles (in fact one is sufficient), the two local oscillators will be well synchronized.

A desynchronization mechanism, as pointed out above, is also needed for a realistic model. It too exists as an intrinsic property of the local oscillator model. Once a channel opens, the current density is locally increased, leading to increased ohmic and diffusion losses which locally reduces the potential across the oxide layer (see Fig. 3a). This reduces the electric field strength in the neighborhood of an active channel, and therefore the probability for a "breakthrough" next to an active pore.

Applied to the example given before, this effect would slow down the dynamics of the oscillator until it is perfectly out of phase. In consequence not all areas of the oxide layer could grow at the same time, which means a desynchronization of the macroscopic oscillation. Assuming a reduction of the current density at a distance r from the channel, the electric field shows the cylindrical geometry of Fig. 3b and the losses for the applied potential are given in a first approximation by

. (4)

As a first approximation this function is used to describe the potential and diffusion losses of the anodic potential in the Monte Carlo simulations, with A as a fitting parameter.

We will now proceed to show that the model described can account for most, if not all observations in the low-frequency domain.

Analytical Results

To summarize, our model contains

Local oscillators caused by oxide growth in an ionic break-through mechanism,

synchronization of local oscillators by next neighbor interaction due to lateral growth at the break-through channel tips,

desynchronization by ohmic or diffusion losses of the anodic potential at local oscillators.

The performance of the model and its dependence on parameters is analyzed by Monte Carlo simulations. But before discussing these general results, some qualitative features and analytical formulae for the case of well synchronized oscillations will be presented.

One important feature of the model is that it provides for a persistent, but changing roughness of the oxide surface as well as the Si-oxide interface. The local oscillators, if active, always produce rather pronounced "bumps" during the oxide-building phase as shown in Fig. 2. The chemical dissolution of the oxide, however, tends to smooth the surface and thus reduces the roughness. This is an important feature with repercussions to the calculation of e.g. capacitance or dielectric constants as obtained by averaging measurements such as ellipsiometry [8]. The Monte-Carlo simulations will provide a detailed and quantitative picture of this process; here we just keep in mind that the speed of a chemical dissolution process depends on surface roughness since it is roughly proportional to the surface area.

For very slow oscillations the time for building up the oxide can be neglected compared to the time for dissolving oxide. This can be seen directly in the current-voltage curves of Fig. 1, where a short current peak corresponding to oxide growth is followed by a long period of low current corresponding to oxide dissolution. The time T for one oscillation period is therefore approximately . Using the electric field defined dynamics for the local oscillators as discussed above, we find

. (5)

This linear correlation between T and U_an is by no means obvious, because for "high-frequency oscillations", which are not included in this model, the reverse is true: The oscillation time decreases with increasing potential [21]. For extremely diluted HF-electrolytes, and thus a slow dissolution rate a, the oscillation time then increases linearly as a function of the applied voltage, as experimentally shown in [4, 22] or in our own measurements (Fig. 4). In addition, the frequency f=1/T should be proportional to a; but this is much more difficult to ascertain experimentally, because changing the HF-concentration and therefore a, also changes other properties of the Si-HF contact. Nevertheless, a linear correlation between the frequency f and the dissolution rate a was found experimentally in [12]. It is also worthwhile to point out that a is the only strongly temperature dependent parameter in Eq. 4. This would allow to make appropriate experiments as a test of the model. As a last remark, we want to point out that a must not be taken as the dissolution rate of "normal" oxide in HF. Due to the persistently rough nature of the oxide surface, the dissolution rate on the average is enhanced by a factor of approximately 1.7 as shown in [14].

For stable oscillations the mean oxide layer thickness does not change, i.e. applying Eq. 1 we find

. (6)

The bar denotes the averaging across the complete electrode area and over one oscillation period. The mean oxidizing current thus is

, or . (7)

Inserting Eq. (6) in Eq. (4) we find

(8)

This correlation between oscillation frequency f and mean current density has experimentally been shown in [14, 22].

The model thus allows to generate the correct relations of observable parameters and agrees qualitatively with experimental results. In the remainder we will demonstrate that with a reasonable set of model parameters, the equations given above supply quantitative data which match perfectly with all experimental data known to us.

Results from Monte Carlo Simulations

a) Implementing the model

Monte Carlo simulations are implemented on a PC and were performed for various sets of model parameter as discussed in the appendix.

Of course, the quantitative results depend on the parameters used to implement the model. The case of extremely diluted hydrofluoric acid with a dissolution rate of a=0.04 nm/s was chosen which was calculated from own experimental data using an electrolyte concentration of 0.05 w% HF in [14]. There are also independent data for a [23] that give values very close to the chosen one, a thus can be considered to be a known parameter for the model.

An assumption has to be made for the critical electric field strengths; we chose E_min=5*10⁶ V/cm and E_max=3*10⁷ V/cm, which not only suits experimental results relating to current transient measurements described in [14], but is compatible with the electronic break-through strengths of thin oxides [24]. Again, admittedly with some more uncertainties as in the case of a, the critical field strengths are in essence known parameters of the model.

We further assume a constant oxidizing current of 0.1 fA through each open channel as discussed in the appendix. This value is determined by the average current density and the geometry of the process and can also be viewed as a known parameter and not a as fit parameter of the model.

More critical is the choice of some appropriate probability functions W(E) and R(E) since not much is known about these function from independent experiments. It is, however, very likely that oxides with rather large breakthrough field strength will not have very "soft" probability functions. Bearing this in mind, we fitted reasonable functions so as to obtain best results - see the appendix for details.

For the desynchronization as described by Eq. (4), we take A=0.2 V nm. This is the only parameter in the model that is mostly determined by fitting, because no independent estimate could be made so far. Fig. 3 shows, roughly to scale, the physical implications of the chosen value. Stable macroscopic oscillations, damped oscillations, unsynchronized oscillations, or no oscillations at all, can be obtained by varying A. We will come back to this parameter in the discussion.

In essence, the model needs three parameters that have to be obtained primarily by fitting model data to experiments.

b) Results

Figs. 5a-d show maps of the oxide layer thickness on an 200nm x 200nm area for subsequent phases of one oscillation period. Most important is the lateral coupling of local oscillators in areas more than 100 nm in size, although there is no mechanism implemented in the model to force such large areas to nearly the same thickness. What happens is that the lateral synchronization of these areas is caused by percolation due to the local coupling mechanism, which in consequence leads to synchronization in the time domain and to macroscopic oscillation. If the anodic potential is reduced, or the parameter A in Eq. (4) (and thus desynchronization) is increased, no macroscopic current oscillations will manifest the still existing local oscillations. The corresponding oxide thickness map s(x,y) of Fig 6 shows a "random" distribution for s(x,y), and the histogram in Fig. 6 may be interpreted as the average of the histograms in the oscillating case of Fig. 5.

The calculated data of the Monte Carlo simulation can be compared with experimental results. First, the thickness distribution of the oxide layer, e.g. the oxide layer distribution function D(s) which determines the total area of the oxide with thickness s, can be directly obtained. Comparing our calculated histograms in Fig. 5a-d with the experimentally determined distribution function given in [14], we find an almost perfect agreement for all phases of the oscillation. It should be emphasized that the calculated and the measured distribution function would be completely independent if only their shape is compared; the agreement of the numerical values, however, is to some extent the result of the fitting of the three parameters mentioned to the absolute thickness values of the oxide as given in [14].

If the same set of parameters employed in the Monte-Carlo simulations is used for Eq. (5), we can calculate, e.g. the frequency of the oscillations as a function of the applied voltage and compare the results with experiments in Fig. 4 The agreement is perfect, providing an independent proof of the validity of our assumptions. Similar results are obtained for the frequency- current relations [22]

Going beyond the analytical formulae and using the distribution function D(s) obtained from the histograms we can now calculate a number of measurable quantities, e.g.

the mean oxide thickness , (9)

the oxide roughness , (10)

the capacitance , (11)

and the ratio (12)

which is the "virtual" change needed for the dielectric constant e of SiO₂, if the capacitance is calculated from the mean oxide thickness according to .

One set of results is shown in Fig. 7A-E. In order to demonstrate the strong synchronization due to next-neighbor interaction and percolation, we chose random starting conditions, i.e. a random distribution of oxide thickness, but this generates only small aberrations in the first period of the oscillations.

The current oscillations obtained from the calculation perfectly match the shape of the experimental curve given in Fig. 1c. To better understand the oscillation process, four points in Fig. 7A, corresponding to specific changes in the oscillation process, are labeled "a" - "d" and will be discussed. The computed images in Fig. 5a-d, correspond exactly to the marked points in Fig. 7A; an interpretation of the particular state of the electrode at the four points is thus possible.

At "a", we find a nearly homogeneous thick oxide layer, which is dissolved with a nearly constant rate a up to about point "b", where first oxide areas show ionic conductivity and are growing quickly while most of the oxide is still thinning. Point "c" marks the phase of the oscillation with maximum oxide current. At this point, about half of the area of the oxide is still only dissolving, while on the other half the oxide has already reached its maximum thickness. In point "d" the cycle is almost closed. Most areas show thick oxide layers and are only chemically dissolved, while some remaining areas with thin oxide suffer ionic breakthrough and increase their thickness. In consequence, whereas the synchronization process is strong enough to produce macroscopic current oscillations, the electrode is far from behaving in a homogeneous manner.

Next, we discuss Fig. 7B, showing the mean thickness of the oxide. As we have to expect, it decreases linearly between "a" and "b", because only chemical etching takes place. The maxima and minima necessarily can not coincide with the current extrema, but can be calculated easily. Since they correspond to ds/dt=0, we find their location at the intersection of the current curve with the mean current J_ox given in Eq. (7). The intersection points are shown in Fig. 7A.

A remarkable feature of the model is its ability to provide data about the surface roughness, Fig. 7C shows that the roughness, as defined in Eq (10), oscillates with a rather large amplitude and almost in phase with the current. If measured with an instrument that is not sensitive on a small scale (nm), but perceives only wavelengths in the 10nm region, a waviness that roughly corresponds to the visual impression of Fig. 5a-d would be detected. A constant change-over between a relatively rough surface thus should not only be observed, but was observed, indeed, by in-situ AFM analysis in [19].

Next, we calculate the capacitance of the system. Fig. 7D shows the result, and, as would be expected, shows that the capacitance increases roughly inversely proportional to the mean oxide thickness. If one just uses the mean oxide thickness, however, to compute the capacitance, the result does not fully agree with the measurements and it must be assumed that the dielectric constant also oscillates. This is so because the total capacitance of parallel capacitors differing in their oxide thickness s, is not determined by 1/<s>, but rather by <1/s>. With the help of the equation

(13)

it is possible to calculate the changes in e that seem to be present (or that are directly measured with an ellipsometer if the raw data are processed on the base of the mean oxide thickness) in measurements reported in [22].

Fig. 7E shows e_virtual. The change of 5% seems to be negligible, but since the variation is given by

(14)

the discrepancy increases strongly for thinner oxide layers obtained, e.g., at the higher frequencies employed in [22]. In essence we claim that e is constant and does not change during an oscillation. Changes observed or computed are due to an averaging procedure that must not be applied for the rough oxides present during oscillations.

Discussion

First, we discuss a possible generalization of the model. Macroscopic oscillations resulted from the interplay of synchronizing and desynchronizing next-neighbor interactions and a percolation process which may spread synchronization over a large area.

Using Fig. 2 we can define a minimum distance d of two channels which can exist a the same moment. The critical field strength E_max has to be reached at d, which depends on the actual thickness, the applied potential, the probability function W(E) and the ohmic losses DU_an(r). If d is large, no third channel can open, before one of the two existing channels is closed, the oxide can not grow homogeneously and is rather rough. In contrast, if d is small, the oxide layer can grow nearly homogeneously, because the semi-spherical oxide-"inclusions" overlap.

It might be useful to find a geometric parameter x(d, _Uan) which determines the ratio between the strength of the synchronization and the desynchronization mechanisms. Tentatively, we define

(15)

Beyond a critical value x_crit, (yet to be determined) we expect macroscopic oscillations, otherwise only colored noise is present. This analytical equation, if justified and worked out, could allow to calculate in a simple and general way if macroscopic oscillations are to be expected, without resorting to Monte Carlo simulation. It may then be used to obtain phase diagrams of oscillating electrode systems.

Next, we critically review the fundamental assumptions of the model. Most basic is the ionic break-through hypothesis with the concomitant rapid oxide growth around the pore tip. No direct confirmation of this mechanism is known to us; it thus must be taken as an essential prediction of the model, verifiable, e.g., with high-resolution electron microscopy or scanning tunnel microscopy. It was already mentioned that the postulated ionic break-through may be inextricably linked with electronic break-through; here we point out that this may be the clue to the understanding of "high-frequency" oscillations which are not included in this model.

The parameters coupled to the ionic break-through are less critical. The exact values of the critical field strengths or of the probability function will, of course, influence the numerical results, but not in a fundamental way. Since the values used are within the region that would be expected from any separate consideration, we hold them to be uncritical.

The parameter A describing the desynchronization process is more critical. A back-of-the-envelope calculation looking at a simple Poisson equation that might pertain to the problem, yields no usable result. Again, the value chosen must be taken as a prediction of the model to be justified either by more involved calculations or by experiments.

The strength of the model comes from two points:

1. It is physically sound and as simple as it can be to describe a complex phenomena, and

2. It reproduces quantitatively a large number of experimental results, which could not be understood at all so far, with just one basic assumption and essentially only one truly fitted parameter.

The model makes a large number of predictions (which we will not all discuss here) that can be tested experimentally and thus is open to verification or falsification as it should be. In addition, it can be taken as a fundamental part of a more involved model that includes oscillation in the "high frequency regime". In this case, the restriction of the model to cases where all of the current produces oxide must be relaxed. It will be necessary to include tunnel currents that flow through the oxide to accommodate, e.g., the infrequent galvanostatic experiments [13] where a constant current is impressed on the electrode and voltage oscillations (in a much more complex shape than current oscillations) are obtained. First attempts at looking a galvanostatic experiments were encouraging and will be published elsewhere.

Finally, we like to point out that our model is applicable to all electrodes - not only Si - where the basic process is an interplay of oxide formation and dissolution.

Appendix

The calculation of the model is performed on two lattices s₁(x,y) and s₂(x,y) which store the coordinates of the upper respectively the lower border of the oxide layer for each point (x,y); e.g. the thickness s(x,y) of the oxide layer is calculated by s(x,y)=s₁(x,y) - s₂(x,y). The time evolution of both lattices is calculated by Monte Carlo simulation which refers to the fact that the dynamics of the occurrence and stop of a "ionic breakthrough channel" is defined by probability functions W(E) and R(E).

Knowing the location of each pore at every moment the growth and dissolution of the oxide is defined by a set of differential equations. A discrete version of these differential equations allows to calculate s₁(x,y,t+dt) and s₂(x,y,t+dt), which is not a statistical process. The details of this calculation will be published elsewhere. Here we only stress some "physical properties" of the implemented differential equations:

The pure chemical dissolution of the oxide-electrolyte-surface s₁(x,y) is defined by the etching rate a. Taking into account the increased area of a rough surface, the dissolution rate is enhanced, which leads to a smoothing of the surface roughness.

Through each open channel we assume a constant current . At each time step dt the semi-spherical inclusion around each channel tip is increased by which defines ds₂(x,y). A current

builds up a sphere with about 5 nm radius within 10 sec, which is in good agreement with our experimental results.

For the dynamics of the channels we define the functions

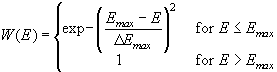(16)

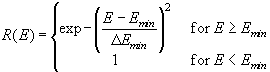(17)

The parameters E_min and E_max define upper and lower limits for the ionic breakthrough mechanism on a area DA in the nm scale within the time Dt. E_min and E_max are comparable to values for a perfect oxide, since the imperfection and inhomogeneity of the anodic oxide is described by the variances DE_min and DE_max. The variances DE_min and DE_max generate the randomness of the model and, in addition to the parameter DU_an, they define the strength of the desynchronization of the local oscillators. To obtain reasonable results for the Monte Carlo simulation we used for E_min and E_max.

a)	b)
c)	d)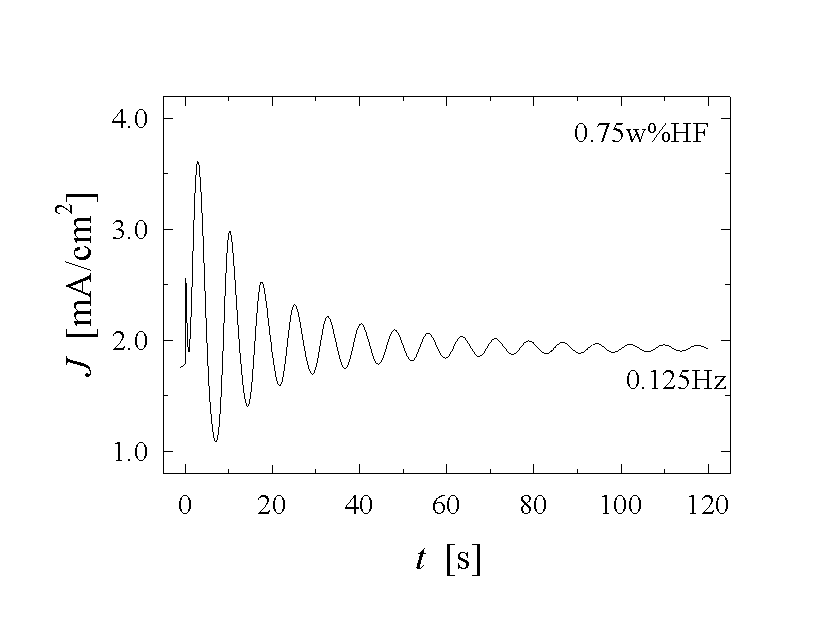

Fig. 1: A set of current vs. time measurements shows different features of the oscillating Si-HF-system. a) - c) applying a constant anodic potential U_an=5 V the frequency and shape of the oscillation differ strongly. Almost chaotic behaviour (a), sine-waves (b), and very asymmetric oscillation (c) are observed. Reducing the potential to U_an=3 V, damped oscillations (d) occur.

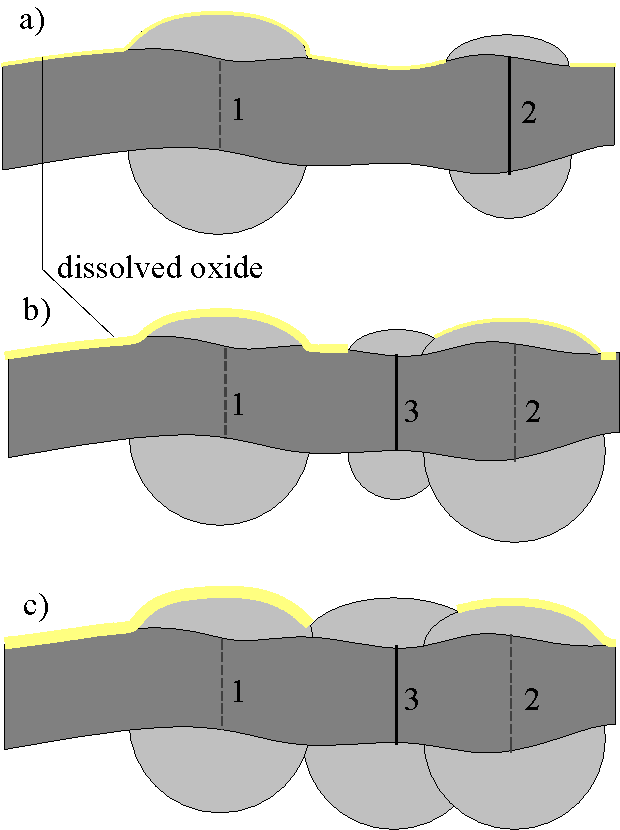
Fig. 2: A highly schematic view of the oxide growth mechanism. a) Channel 1 is already "closed" while channel 2 is "open". Both pores are growing independently because they do not overlap. b) A third channel opens between channel 1 and 2 if the desynchronization is small, i.e. the anodic potential at channel 3 is not too much decreased by the current through channel 2. c) The closing of channel 3 is early and thus synchronized to channel 1 and 2, because channel 3 needs to grow less oxide for the "closing" to take place. This mechanism leads to a nearly homogeneous growth of the oxide layer. The chemical dissolution occuring all the time (shown, roughly to scale, by the lightly shaded areas) smoothes the surface even more.

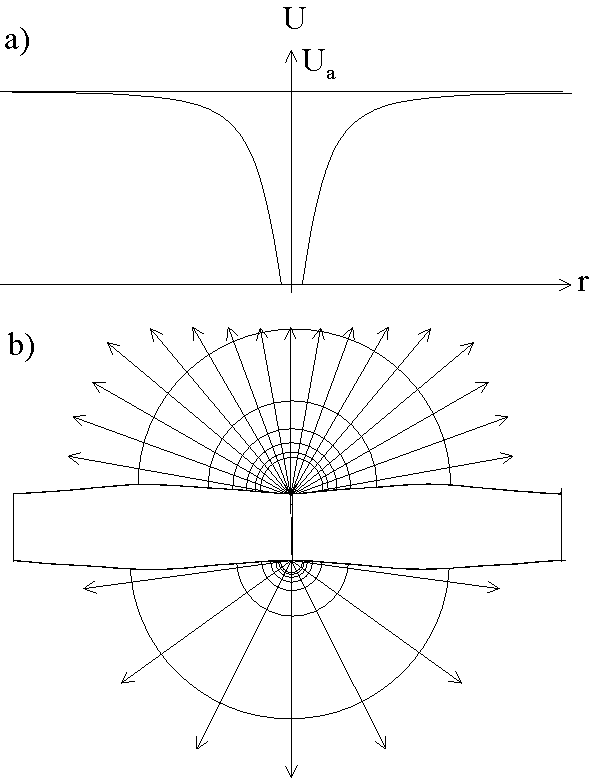
Fig. 3: The decrease or losses DU_an(r) of the anodic potential due to high local current densities are plotted in (a) as a function of the distance r from a break-through channel. b) The corresponding current field and equipotential lines needed to obtain a field strength that decreases by on both ends of the channel. The schematic drawing is roughly to scale relative to the oxide thickness.

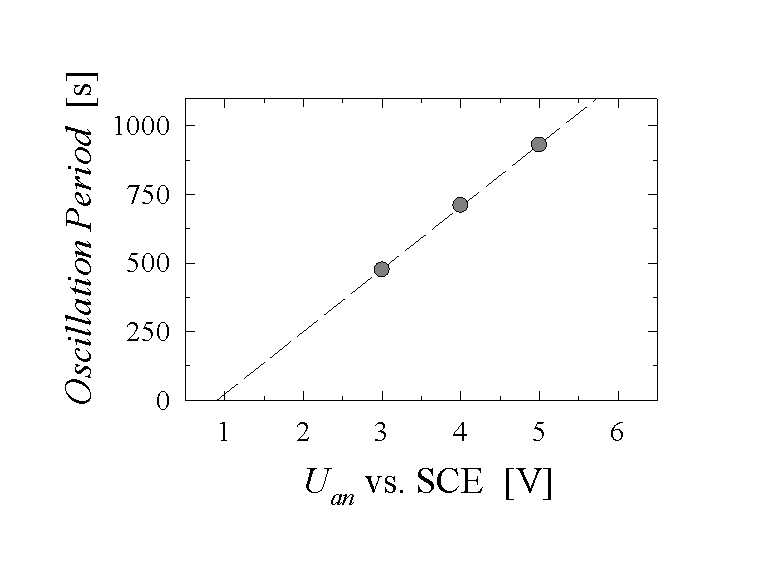
Fig. 4: For extremely slow current oscillations the oscillation period is measured as a function of applied anodic potential. We find a straight line in agreement with Eq. (5).

Fig. 6: The map of the oxide layer thickness for a non oscillating macroscopic current shows no percolation areas. The distribution function of the oxide layer thickness may be interpreted as the average of the distribution functions of a macroscopically oscillating system.

Fig. 5a-5d: A series of "snapshots" of the oxide layer thickness obtained by Monte Carlo simulations demonstrates the strong coupling due to percolation of the oxide layer thickness. The calculated histograms are compared with the measured distribution functions of the oxide layer thickness reported in [12].

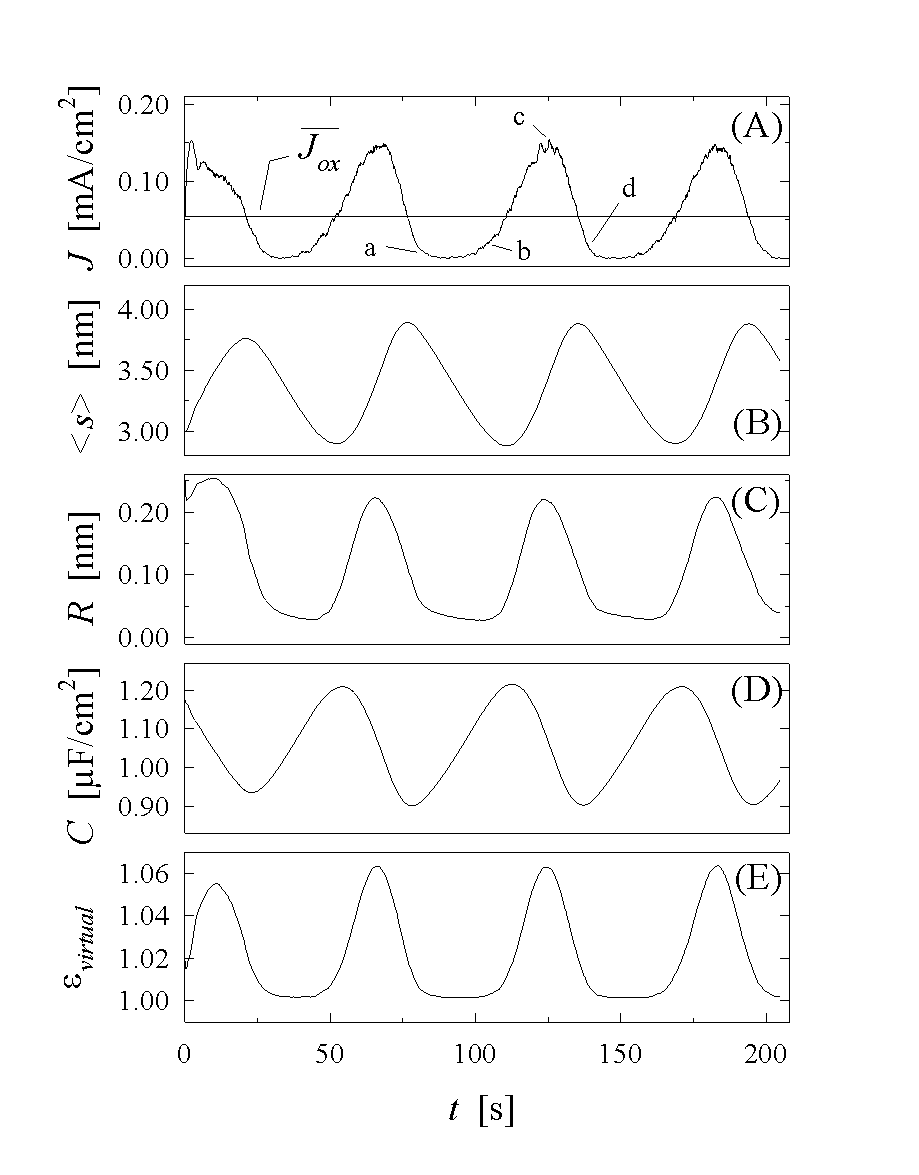
Fig. 7: As a result of the Monte Carlo simulation, current (A), mean oxide thickness (B), surface roughness (C), capacitance of the oxide layer (D) and the relative change in the dielectric constant e_virtual are plotted as a function of time. In graph (A) distinct times of the oscillation are marked corresponding to the maps in Fig. 5a)-d). The average oxidation current density equals the current density J whenever ist capacitance C_ox is maximal or minimal.

References

1. R.L. Smith and S.D. Collins, J. Appl. Phys., 71, R1 (1992)

2. H. Föll, Appl. Phys. A, 53, 8 (1991)

3. D.R. Turner, J. Electrochem. Soc., 105, 402 (1958)

4. H. Gerischer and M. Lübke, Ber. Bunsenges. Phys. Chem., 92, 573 (1988)

5. M. Faraday, Phil. Trans. Roy. Soc London, Ser. A, 124, 77 (1834)

6. V. Lehmann and U. Gösele, Appl. Phys. Lett., 58, 856 (1991)

7. L.T. Canham, Appl. Phys. Lett., 57, 1046 (1990)

8. J. Stumper, R. Greef, and L.M. Peter, J. Electroanal Chem., 310, 445 (1991)

9. F. Ozanam, J.-N. Chazalviel, A. Radi, and M Etman, J. Electrochem. Soc., 139, 2491 (1992)

10. J.-N. Chazalviel and F. Ozanam, J. Electrochem. Soc., 139, 2501 (1992)

11. D.J. Blackwood, A. Borazio, R. Greef, L.M. Peter, and J. Stumper, Electrochimica Acta, 37, 889 (1992)

12. H.J. Lewerenz and M. Aggour, J. Electroanal. Chem., 351, 159 (1993)

13. V. Lehmann, J. Electrochem. Soc., 143, 1313 (1996)

14. J. Carstensen, R. Prange, G.S. Popkirov, and H. Föll, Appl. Phys. A, in press

15. H.J. Lewerenz, Chem. Soc. Rev., 26, 239 (1997)

16. U.F. Franck, Angew. Chem., 90, 1 (1978)

17. J.-N. Chazalviel, F. Ozanam, M. Etman, F.Paolucci, L.M. Peter, and J. Stumper, J. Electroanal. Chem., 327, 343 (1992)

18. M. Aggour, M. Giersig, and H.J. Lewerenz, J. Electroanal. Chem., 383, 67 (1995)

19. O. Nast, S. Rauscher, H. Jungblut, and H.J. Lewerenz, J. Electroanal. Chem., in press

20. J.-N. Chazalviel, Electrochimica Acta, 37, 865 (1992)

21. often observed, but not published except in: V. Lehmann, PhD thesis, Erlangen (1988)

22. F. Ozanam, J.-N. Chazalviel, A. Radi, and M. Etman, Ber. Bunsenges. Phys. Chem., 95, 98 (1991)

23. C. Serre, S. Barret, and R. Hérino, J. Electrochem. Soc., 141, 2049 (1994)

24. D.J. Dumin, J. Electrochem. Soc, 142, 1272 (1995)