Lösung zur Übung 10.1-3

Kennlinien und Probleme realer Solarzellen

	Hier ist der Ausgangsgspunkt für die Lösung der Aufgabe:
		I  =  I1 ·  æ ç è exp  eUpn kT   –  1 ö ÷ ø   +  Upn RSH  –  IPh Upn =  U – I · RSE
	Diskutiere (qualitativ, wo nicht anders gefordert) den Einfluss der beiden Widerstände auf die Kennlinie. Betrachte zunächst nur die Grenzfälle mit RSE = 0 W bzw. R SH Þ ¥ W. Beschreibe den Einfluss dieser Widerstände einzeln (und dann zusammen) auf Leerlaufspannung Kurzschlusstrom Sperrstrom im Dunkeln Füllfaktor Wirkungsgrad
		Das ist ein umfangreiches Programm; aber machbar:

Serienwiderstand R_SE

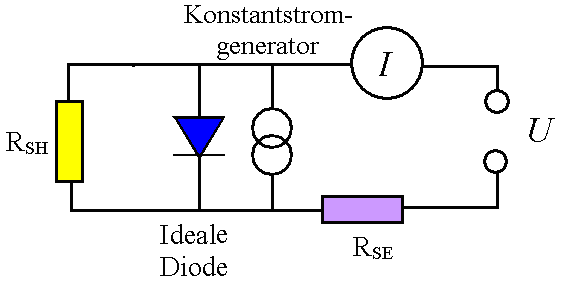
	Für einen erstmal vernachlässigbaren Shuntwiderstand RSH können wir leicht ein paar qualitative Fakten deduzieren:
		Für I = 0 A haben wir Upn = U. Das bedeutet, dass alle IU Kennlinien auf der Spannungsachse durch UOC laufen müssen.
		Für große negative U (also Sperrrichtung) ist I schlicht konstant. Wir verlieren einen Teil der Spannung im Serienwiderstand, aber das macht nichts. Die Kennlinie im 3. Quadranten hängt damit nicht von RSE ab sofern |U| groß genug ist.
		Für große positive U (also Vorwärtsrichtung) würde die ideale UOC » 0.5 V Diode oberhalb von ca. 0.5 V sehr große Ströme durchlassen, oder anders ausgedrückt, der Diodenwiderstand (Rdiode = dU/dI) der idealen Diodenkennlinie wird sehr klein. Mit einem merklichen Serienwiderstand RSE > Rdiode wird die IU Kennlinie vom Serienwiderstand dominiert werden, d.h. sie degeneriert zu einer Geraden mit Steigung 1/RSE .
		Im interessierenden 4. Quadranten für Spannungen kleiner als U OC fällt ein Teil der Spannung im Serienwiderstand ab. Der pn-Übergang hat weniger Spannung, der Strom kann also (betragsmäßig !) nur kleiner sein als bei der Kennlinie ohne Serienwiderstand. Aufpassen! Mit Vorzeichen ist er größer, denn -3 ist größer als -5!
	Setzt man das alles zusammen, muss man qualitativ Kennlinien erhalten, wie im folgenden Bild (sauber numerisch gerechnet!) gezeigt.
		Die Kennline zeigt unsere Referenz- Solarzelle mit Zahlen an den Achsen. Zumindest für die größeren Serienwiderstände sollte auch díe qualititave Lösung so ähnlich aussehen
	Wir können damit eine Reihe von Schlussfolgerungen ziehen
		1. Der Wirkungsgrad h ist proportional zu ISc · UOC · FF. Für nicht zu große Serienwiderstände (im Beispiel oben RSE < 100 mW) verringert ein Serienwiderstand also primär den Füllfaktor und reduziert damit den Wirkungsgrad h.
		2. Während im normalen "elektrotechnischen" Leben Widerstände im Milliohmbereiche so gut wie keine Rolle spielen, sind hier einige mW schon deutlich spürbar.
		3. Mit dem gegebenen spezifischen Widerstand bester Metalle von ca. r » 2 µWcm sieht man, das ein 1 cm langer Cu Draht mit einem 1 mm2 Querschnitt bereits einen Widerstand von R = 2 mW hat. Das bedeutet: Wir haben schon bei der Kontaktierung (dem "Grid" auf der Solarzelle) ein massives Problem mit Serienwiderständen realer Solarzellen!

Shunt Widerstand R_SH

	Für einen vernachlässigbaren Serienwiderstand können wir leicht ein paar qualitative Fakten deduzieren:
		Es gilt immer Upn = U. Für Upn = U = 0 V müssen alle Kennlinien durch ISC laufen, da Upn/RSH = 0.
		Ansonsten haben wir alle Spannungen U in Rückwärts- und Vorwärts richtung den Strom I SH = Upn/RSH der zum Diodenstrom (vorzeichenrichtig) addiert werden muss. Das schiebt den Kennlinienstrom um Upn/RSH "nach oben" zu kleineren Absolutwerten und größeren "Vorzeichen"-Werten (siehe oben). Die vorher flache Kennlinie wird steil mit der Steigung 1/RSH
		Im 4. Quadrant, auf den es ankommt, verlieren wir Spannung und Füllfaktor, damit geht der Wirkungsgrad h kräftig runter.
		Darüber hinaus nimmt der (Betrag) des Sperrstroms linear mit der Sperrspannung zu. Das ist ein großes Problem sobald unsere Solarzelle mit anderen verschaltet wird, d. h. in einem Solarmodul.
	Hier sind die entsprechenden (wieder sauber numerisch berechneten) Kennlinien. Auch qualitativ muss man auf einen solchen Graphen kommen.
	Wir können wieder einige Schlussfolgerungen ziehen:
		1. Der Wirkungsgrad h ist proprotional zu ISc · UOC · FF. Falls RSH nicht zu klein wird (im Beispiel >» 1W), sind Shunts nicht allzu schlimm. Andererseits sind richtige Kurzschlüsse (R SH < » 1W) tödlich.
		2. Da Solarzellen sehr ausgedehnte pn-Übergänge haben, die außerdem noch bis zur "Kante" reichen, müssen wir mit vielen kleinen " Kurzschlüsschen" rechnen. Wie eine Reihe von kleinen lokalisierten "Kurzschlüsschen", die jeder für sich nicht viel Böses tun, die Gesamt-Solarzelle beeinflussen, die wir hier betrachten, ist ein trickreiches Problem (man kann sie nicht einfach "aufaddieren").

Mit Frame

10.1.2 Die reale Solarzelle

Übung 10.1-3

© H. Föll (MaWi für ET&IT - Script)