9.5.2 Was man wissen muss

	Wir kennen auswendig, weil verstanden, die wichtigsten Gleichungen für reale (= dotierte) Halbeiter im Gleichgewicht.
		nMaj  =  NDot nMin(T)  =  ni2(T) NDot    R  =  G  =  nMin t
		Wir wissen, dass bei Si die Energielücke E G = 1,1 eV beträgt.
		Wir haben ein Gefühl für Dotieren : Womit (in Si: P und As für n-Typ, B für p-Typ), wieviel man so nimmt (1015 cm–3 . . . 1019 cm–3 ), und wie's ungefähr gemacht wird.
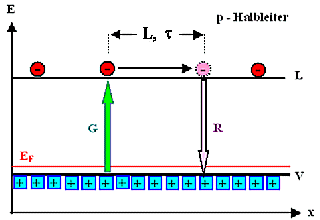
		Wir wissen, was Generationsrate G, Rekombinationsrate R und Lebensdauer t bedeuten. Löcher im Valenzband und Elektronen im Leitungsband sowie ihr Verhalten bezüglich Energie und Feld sind uns vertraut.
	Was in den nachfolgenden Bildern / Gleichungen gezeigt ist, haben wir also total verstanden:
		R  =  nMin t   = G L  =  (D · t)½
		Wir wissen, was direkte und indirekte Halbleiter unterscheidet, und dass Si ein indirekter Halbleiter ist.
	Der Weg zu diesen Erkenntnissen war steinig.
		Wir könnten aber noch Gleichungen wie die unten gegebenen zumindest zuordnen, und wir haben vor allem verstanden, was die Position der Fermienergie in der Bandlücke bestimmt – und warum das so wichtig ist.
		ne   =  ¥ ó õ EL   D(E) · f(E; EF, T) · dE               »  Neff   · exp( – EL – EF kBT   ) n h   =  EV ó õ –¥   D(E) · [1 – f(E; EF, T)] · dE                 »  Neff   · exp(  – E F – EV kBT  ) ne · nh = ni2 ni     =  Neff  · exp( –  EG 2kBT  )
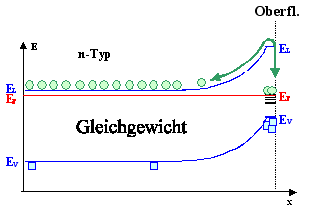
	Bandkrümmungen wie dargestellt sind (semi-)quantitativ und qualitativ verstanden.
	Wir wissen, dass zwischen der Beweglichkeit µ und dem Diffusionskoeffizienten D der Ladungsgträger eine simple Beziehung existiert und erinnern uns zumindest an µ µ D.
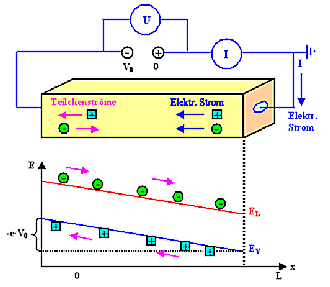
		Damit ist die Leitfähigkeit s = qnµ der Halbleiter klar, und auch wie sie im Prinzip von der Dotierkonzentration NDot abhängt.
	Die Bedeutung von Kontakten ist klar; wir können einige konstruieren, denn wir kennen das 3-Schritte-Rezept.
		Der Zusammenhang zwischen Ladungen, Bandverbiegung , Raumladungszone und elektrisches Feld im Kontakt ist klar.
		Das Kondensatormodell für die Weite der Raumladungszone ist klar; mit einigen Hinweisen könnten wir es rekonstruieren.
	Wir können das Banddiagramm eines pn-Übergangs konstruieren, Ladungsträger und Ströme einzeichnen, die Ströme benennen und auch noch die Ladungsverteilung im Ortsraum skizzieren (wir sehen auch, dass im Bild unten was vertauscht ist gegenüber dem darüber).
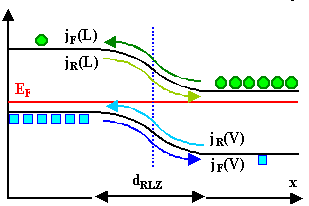		Strom der Majoritäten in das jeweils andere Gebiet: Diffusionsstrom oder Rekombinationsstrom oder Durchlaßstrom. Beispiel: Elektronenstrom vom n-Si zum p-Si. (Hinweis: In dieser Abbildung sind die Teilströme noch englisch beschriftet: Diffusionsstrom = forward current jF, Feldstrom = reverse current jR) 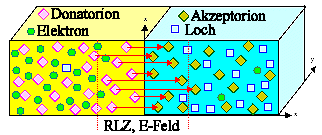Strom der Minoritäten in das jeweils andere Gebiet: Feldstrom oder Driftstrom oder Generationsstrom oder Sperrstrom. Beispiel: Elektronenstrom vom p-Si zum n-Si.
		Wir haben im Detail verstanden, dass im Gleichgewicht gilt:  jD = –jF  und   |jF| = e · L · G = e · L · ni2/t · NDot
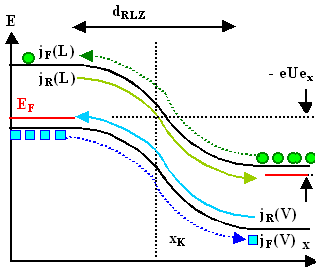
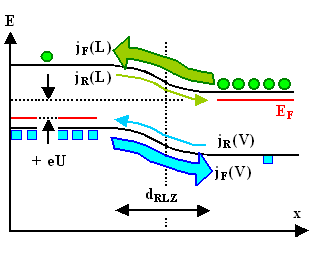
	Wie die Banddiagramme mit externer Spannung ausssehen und wie daraus die Diodengleichung folgt, ist klar (Hinweis: In der folgenden Abbildung sind die Teilströme noch englisch beschriftet: Diffusionsstrom = forward current jF, Feldstrom = reverse current jR).
		j( Uex)  =   æ ç è e · L · (ni )2 NA · t + e · L · (ni)2 ND · t ö ÷ ø · æ ç è exp( eUex kBT ) – 1 ö ÷ ø
	Wenn bis dahin wirklich alles klar ist, versteht sich der Rest von selbst.

© H. Föll (MaWi für ET&IT - Script)