|
Die einfache Formel für die Ladungsträgerdichte (effektive
Zustandsdichten und Boltzmann-Näherung
) in intrinsischen Halbleitern ist ziemlich gut. | |
| ne » |
Neff · exp( – |
EL – EF
kBT |
) | | | |
| | |
nh » |
Neff · exp(– |
E F – EV
kBT |
) |
|
|
|
 |
Wir werden deshalb nur noch mit dieser Formel rechnen (bis wir eine noch einfacherer
Formel haben werden). Þ | |
|
 |
Für die jetzt vertrauten Löcher ergeben sich
(immer mit entsprechendem Vorzeichenwechsel) völlig symmetrische Beziehungen. | |
| | |
| |
 |
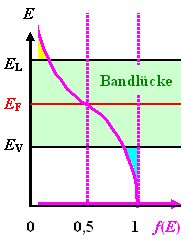
Die Fermieenergie
EF für intrinsische Halbleiter folgt aus n
e=n h oder – allgemeiner – der notwendigen Ladungsneutralität. |
|
|
|
 |
Die Fermienergie liegt in der Mitte der Bandlücke. | |
|
 |
Das läßt sich sowohl leicht errechnen, als auch graphisch sofort erkennen: Die
"Zwickel" müssen gleich groß sein. | |
|
 |
Der gezeigte Fall, daß die "Zwickel" so weit in die Bänder hineinragen,
entspricht der Eigenleitung; sie tritt bei Temperaturen auf, für die 4 kBT
≥ Eg gilt. | |
|
| | | |
 |
Löcher benehmen sich im wesentlichen wie positiv
geladene Elektronen. Ihr Beitrag zur Leitfähigkeit ist damit Þ
| |
| sh |
= |
+e · nh · m h |
| | |
| | s
total | = |
se + sh
» 2s e |
|
|
|
 |
Löchern kann neben einer Dichte und einer pos. Ladung auch eine Beweglicheit
mh zugeordnet werden; sie ist ähnlich zu der der Elektronen. |
|
|
 |
Während Elektronen, wenn sie können, energetisch tiefer sinken, steigen Löcher
aber auf - wie Luftblasen im Wasser! | |
| |
| | |
|
 |
Das Massenwirkungsgesetz
ergibt sich aus obigen Konzentrationsgleichungen; es ist sehr wichtig! | |
|
| | Halbleiter |
Ge |
Si |
GaAs |
| Energielücke [eV] | 0,661 | 1,12 |
1,424 | | ni (RT) [cm–3] |
2·1013 |
1·1010 |
2,1·106 |
|
|
 |
Dabei ist n i=ne=n h
die intrinsische Ladungsträgerdichte für ideal-perfekte Halbleiter,
bei denen Elektronen- und Löcherkonzentration per definitionem gleich groß sind. | |
|
 |
n i ist eine Materialkonstante
, direkt verknüpft mit der Energielücke E
G. | |
|
| | | |
 |
Legt man eine Spannung U an einen Halbleiter, addiert (oder, je
nach Vorzeichen, subtrahiert) man die Energie eU. | |
|
|
 |
Die Bandkanten rutschen entsprechend hoch oder tief | |
|
 |
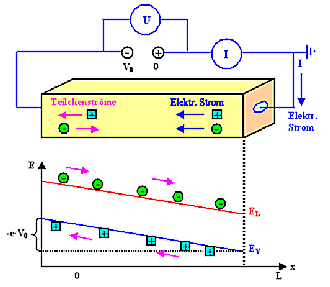
Fällt die Spannung gleichmäßig über den Halbeiter ab, erhält man
eine Bandverbiegung wie gezeigt. Þ | |
|
 |
Entscheidende Punkte sind:
- Leitungs- und Valenzband sind "verbogen".
- Grund: Zusätzliches elektrisches Potential.
- Verbiegung=elektrisches Feld E.
- Elektronen laufen abwärts, Löcher aufwärts.
- Falls Nettostrom, kein Gleichgewicht mehr.
- Gründe für Bandverbiegungen sind: Nettoladungen irgendwo im System.
| |
| |
| | | |
 |
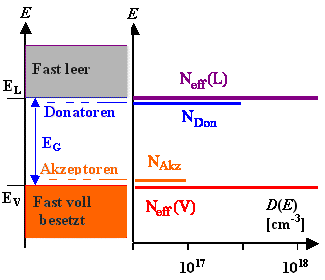
Dotieren=gezieltes Einbringen von Dotierstoffen
(als substitutionelle Fremdatome) mit Elektronenzuständen in der Energielücke dicht an den Bandkanten. |
|
|
|
 |
Donatoren (in Si entweder P oder As)
haben einen am Atom lokalisierten besetzten
Zustand dicht unterhalb der Leitungsbandkante. Das dort "sitzende" Elektron kann leicht ins Leitungsband
springen und ist dann frei beweglich . Zurück bleibt ein ortsfestes
positiv geladenes P+ -Ion. | |
|
 |
Akzeptoren (in Si immer B) haben einen
am Atom lokalisierten unbesetzten Zustand für Elektronen dicht oberhalb
der Valenzbandkante. Elektronen aus dem Valenzband können leicht auf diesen Zustand springen und ihn besetzen.
Wir haben insgesamt ein frei bewegliches Loch im Valenzband und ein negativ geladenes
ortsfestes B–-
Ion. | |
|
| | | |
 |
Entscheidend ist, wie immer, die Lage der Fermienergie. |
|
|
|
 |
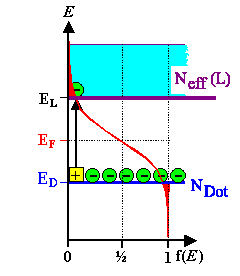
Bei n-Dotierung kommen für kleine T alle Elektronen in L von den
Dotierniveaus; EF muss zwischen Dotierniveau E
D und dem Leitungsband sitzen. | |
|
 |
Das gilt auch noch bei höheren Temperaturen: E F ist in der
Nähe des Dotierniveaus. | |
|
 |
Wir haben mit Dotieren sehr viel mehr Ladungsträger einer Sorte als im undotierten intrinsischen
Halbleiter, bei dem beide Dichten gleich groß sind. | |
| | |
| | |
|
 |
Die Dichte nMaj der Majoritätsladungsträger
ist in Si bei RT in guter Näherung identisch zur Dichte der Dotieratome NDot
. | |
| | |
|
| n Maj
|
= |
N
Dot | | |
| |
|
nMin (T) |
= |
ni2
(T)
NDot |
| | |
|
|
|
|
 |
Die Dichte der Minoritätsladungsträger
n Min folgt aus dem Massenwirkungsgesetz
. | |
|
 |
Donatoren:
P und As Þ n-Si
Þ Majoritäten sind Elektronen im Leitungsband.
Minoritäten sind Löcher im Valenzband. | |
|
 |
Akzeptoren: Nur B Þ
p-Si
Þ Majoritäten sind Löcher im Valenzband.
Minoritäten sind Elektronen im Leitungsband. | |
| | |
| | |
 |
Beweglichkeiten sind an Stöße gekoppelt. Wichtige Stoßpartner
waren "Phononen" (=thermische Gitterschwingungen) und Kristalldefekte. | |
|
|
 |
Dotieratome sind Defekte. Sie verringern damit die Beweglichkeit (und damit die
Leitfähigkeit ein bißchen) aber erhöhen die Ladungsträgerdichte (und damit die Leitfähigkeit enorm) |
|
|
 |
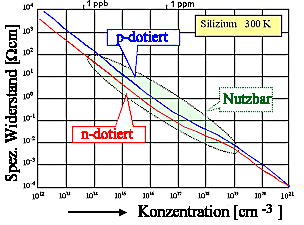
Der Gesamteffekt der Dotierung von Si bei RT ist in der Masterkuve gezeigt:
Þ | |
|
 |
Die "Beulen" im ansonsten ziemlich linearen Verlauf kommen von der Änderung
der Beweglichkeit mit N
Dot; die Unterschiede zwischen n- und p-Dotierung stammen von verschiedenen Beweglichkeiten
der Löcher und Elektronen. | |
| |
| | | |
 |
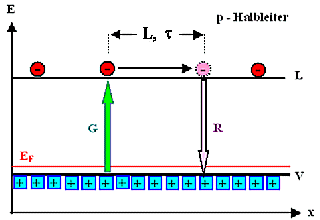
Ladungsträger in den Bändern werden durch Generation
erzeugt (immer thermisch, bei Beleuchtung auch durch Licht), laufen etwa eine Diffusionslänge weit per "random
walk" durch den Kristall, und verschwinden wieder durch Rekombination. |
|
|
|
 |
Beide Prozesse werde durch Raten beschrieben; Maßeinheit: s–1cm–3
G=Generationsrate
R=Rekombinationsrate | |
|
 |
Da im Gleichgewicht die Ladungsträgerdichte konstant ist, muss gelten: G=R
sowohl für Minoritäten, als auch für Majoritäten. | |
| | |
| |
 |
Von Interesse ist vor allem die Rekombinationsrate RMin
der Minoritäten, da Änderungen der Ladungsträgerdichte bei den Minoritäten sehr viel stärker "durchschlagen" |
|
|
|
| Im Gleichgewicht: |
| G=R =
| nMin
t |
|
|
|
|
 |
Es gilt unmittelbar Þ | |
|
 |
Dabei ist t
die Minoritätsladungsträgerlebensdauer (kurz Lebensdauer); leicht zu visualisieren und mit der Diffusionslänge
L gekoppelt durch Þ | |
|
 |
Daraus folgt die dritte wichtige Halbleitergleichung Þ
| |
| |
| | | |
 |
Es gibt bezüglich der Rekombination zwei Arten von Halbleitern. |
|
Direkte Halbleiter:
L und t sind klein
(ungefähr ns / µm)
Prominente Vertreter: GaAs, InP, GaN.
Indirekte Halbleiter:
L und t sind groß und stark defektabhängig
(ungefähr µs . . . ms / 500 µm)
Prominente Vertreter: Si, Ge, SiC.
|
|
|
 |
Direkte Halbeiter: Rekombination ist leicht; die Überschussenergie
produziert ein Photon, d.h. es wird Licht mit hn=EG
emittiert.
Direkte Halbleiter sind die Grundlage für die Optoelektronik
| |
|
 |
Indirekte Halbeiter: Rekombination ist schwer; die Überschussenergie produziert
Phononen, d.h. es wird Wärme erzeugt.
Silizium ist ein indirekter Halbleiter. | |
| | |
| | |
 |
Kontakte oder "junctions" machen Bauelemente. |
|
|
|
 |
Es gibt kein Halbleiterbauelement ohne Halbleiter-Metall-Kontakt
und so gut wie keines ohne "pn-Kontakt". | |
|
 |
Kontakte bei Halbleiterbauelementen macht man nicht durch "kontaktieren" im Sinne
von "Zusammendrücken", sondern durch (extrem trickreiche) Halbleitertechnologie. | |
|
 |
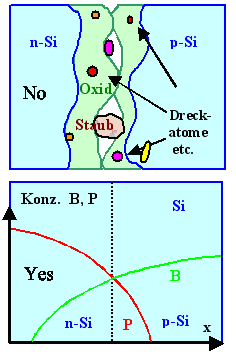
Ein pn-Kontakt liegt vor an der Stelle, an der die Akzeptor- und Donatorkonzentration
gleich groß ist. | |
|
 |
"Ohmsche Kontakte", die man immer braucht, sind
idealerweise eigenschaftslos, d. h. sie lassen bei jeder Spannung und Polarität den vollen Strom durch. Sie sind aber
oft recht schwer zu machen. | |
|
| | | |
 |
Links und rechts von einem Kontakt können vor Kontakt unterschiedliche Fermienergien
vorliegen. | |
|
|
 |
Þ Es gibt unterschiedliche Ladungsträgerkonzentrationen. |
|
|
 |
Þ Es gibt unterschiedliche Zustände in der Energielücke bei "homo"-Kontakten
wie dem Si pn-Übergang. | |
|
 |
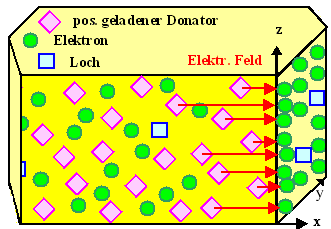
Beispiel: "Kontakt" Si mit der Oberfläche
des Si Kristalls. | |
 |
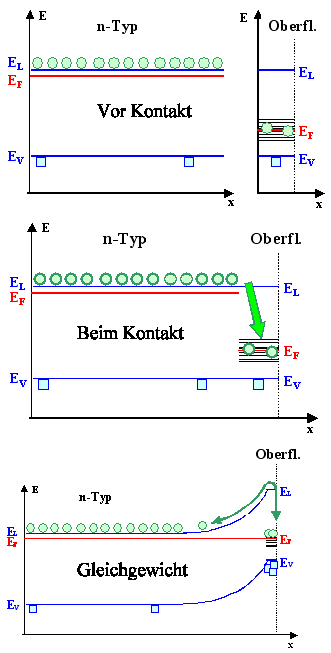
Es ist extrem wichtig, das Bild Þ
zu verstehen! | |
|
 |
Vor Kontakt: "Irgendwie" verschiedene Si - Varianten=verschiedene Zustände
in der Energielücke=verschiedene Fermienergien. | |
|
 |
In der (Pico)sekunde nach (gedachtem) Kontakt fließen Elektronen auf jetzt verfügbare
Zustände mit niedrigerer Energie (im Beispiel nach rechts zu den Oberflächenzuständen); Löcher laufen
auf neu verfügbare (mit Elektronen besetzte) Plätze mit höherer Energie. | |
|
 |
In der Nähe des Kontakts herrscht keine Ladungsneutralitität mehr. Im Beispiel lädt
die Oberfläche sich negativ auf durch den Zustrom von Elektronen, die jetzt aber auf
der Oberfläche lokalisiert sind. | |
|
 |
Im Volumen nahe der Oberfläche bleiben díe ortsfesten positiv geladenen Donatoratome
zurück; sie bilden eine Raumladung mit der Dichte ND+. |
|
|
 |
Dadurch entsteht ein elektrisches Feld, das die zur Oberfläche
strebenden Elektronen zurücktreibt. | |
|
 |
Die rechte Seite des Banddiagramms geht deshalb energetisch "hoch", es entsteht
eine Bandverbiegung. | |
| | |
| | |
 |
Entscheidend ist das Banddiagramm für Gleichgewicht.
Einige Definitionen dazu, die alle im Grunde dasselbe sagen: | |
Ü Vollständig äquivalente
Formulierungen
Damit Rezept für Banddiagramm-Erstellung: |
| 1. |
Zeichne die Fermienenergie als horizontale Linie;
markiere den Kontakt. |
| 2. |
Zeichne "weit" links vom Kontakt das Banddiagramm von Material 1, weit rechts das von Material
2 –
immer relativ zu der bereits festgelegten Fermienergie. | | 3. |
Verbinde Leitungs- und Valenzband
durch eine "gefühlsmäßig" gezeichnete Bandverbiegung.
|
|
|
 |
Gleichgewicht liegt vor, sobald es genau so viel Energie kostet, gegen das Feld anzulaufen,
wie man durch "Tieferfallen" an der Oberfläche gewinnen kann. | |
|
 |
Gleichgewicht liegt vor, sobald energetisch nichts mehr
zu gewinnen ist. Þ Die Fermienergie ist überall dieselbe. |
|
|
 |
Gleichgewicht liegt vor, sobald der nach rechts fließende
Elektronenstrom genau so groß ist wie der zurückfließende Strom.
| |
|
 |
Ströme fließen, weil es für Elektronen auf beiden Seiten eine Wahrscheinlichkeit
exp[–DE/(kBT)] gibt, die
Energiebarriere
DE zur jeweils anderen Seite zu überwinden. |
|
| | |
| | |
 |
Eine Darstellung im Ortsraum verdeutlicht
das Konzept der Raumladungszone. | |
|
|
 |
Es gibt "Ladungen im Raum", da die ionisierten Dotieratome nicht beweglich sind
und "ihre" Ladungsgträger jetzt woanders sind. | |
|
 |
Das elektrische Feld beginnt und endet auf den jetzt separierten
Ladungen. | |
|
 |
Wir haben unvermeidlich einen geladenen Kondensator
mit der Kapazität CRLZ. | |
| | |
| |
 |
Die Weite dRLZ der Raumladungszone (RLZ
oder "SCR " für "space charge region") ergibt sich sofort aus dem Kondensatormodell: |
|
| CRLZ |
= |
2 · eSi ·
e0 · F
dRLZ |
| CRLZ | = |
Q
UK |
= | Q
DEF/e |
| | | |
| | |
= |
e2 · (ND · F
· dRLZ)
DEF |
| d RLZ |
= |
æ
ç
è |
2 · er · e
0 · DEF
e2 ·N
D | ö
÷
ø
| ½ |
|
|
|
 |
Wir haben Fläche F und (mittleren) Abstand der "Kondensatorplatten"=½dRLZ
| |
|
 |
Der Potentialunterschied in Volt=anliegende Spannung
ist DEF/e | |
|
 |
Die Ladung
auf den Platten ist gleich der Zahl
der ionisieten Dotieratome=gleich Dichte mal Volumen
=ND · V der positiv geladenen Donatorionen im Volumen V=F
· dRLZ . | |
|
 |
Aus den beiden Gleichungen für die Unbekannten dRLZ
und C RLZ folgt sofort die Weite der RLZ
Þ | |
| |
| | | |
 |
Legt man zusätzlich zu der "eingebauten" Spannung oder Kontaktspannung D
EF/e noch ein externe Spannung Uex an, muss die Gesamtspannung U
in die Formel eingesetzt werden
(Auf Vorzeichen aufpassen!) | |
|
|
| dRLZ |
= |
æ
ç
è
|
2 e Si
e0 (DEF + eUex)
e2 · ND |
ö
÷
ø |
½ |
| | |
| |
| |
CRLZ
F |
= |
æ
ç
è
|
2 eSi
e0 e2 ND
DEF + eUex |
ö
÷
ø |
½ |
|
|
|
 |
Falls jetzt Strom fließt, haben wir kein Gleichgewicht
mehr! | |
|
 |
Falls kein (oder nur vernachlässigbar kleiner) Strom
fließt, haben wir jetzt Þ | |
| | |
| | |
 |
Formal-mathematisch wird die Poisson-Gleichung
gelöst (Grundgleichung der Elektrostatik). | |
|
|
 |
Die Poisson-Gleichung beschreibt den Zusammenhang zwischen Ladungsdichte r,
elektr. Feld E und elektr. Potential V (bzw. φ). | |
| | |
| |
|
|
| DV(x, y, z) | = –
| r
ee0 | |
| | | |
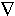 V(x, y, z) V(x, y, z) | = |
– E(x, y, z) |
|
| |
| | |
| |
 |
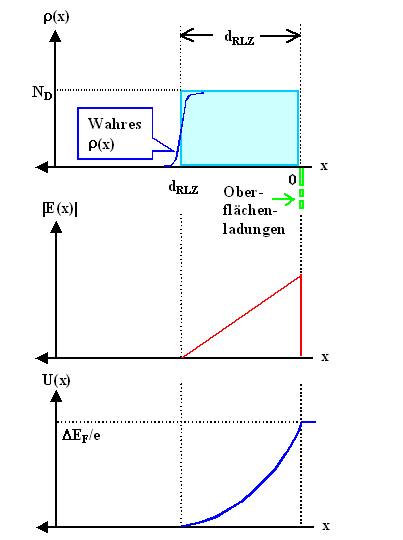
Lösungsweg eindimensional: | |
|
 |
Ladungsdichte
r=NDot
in dRLZ=const. | |
|
 |
Feld
E=einmal integrieren=Gerade. Randbedingung: E(x =d SCR)=0 V/cm |
|
|
 |
Potential
V=zweimal integrieren=Parabel. Randbedingung V(dSCR)=0 eV; Potentialdifferenz=DEF/e | |
| | |
| | |
 |
Das Banddiagramm eines pn-Übergangs im Gleichgewicht folgt sofort
aus der Konstruktionsanleitung: | |
(Hinweis: In
dieser Abbildung sind die Teilströme noch englisch beschriftet: Diffusionsstrom=forward current jF, Feldstrom=reverse
current jR) |
|
|
 |
Fermienergie ist überall gleich. |
|
|
 |
Weit links und rechts vom Übergang liegt das Banddiagramm des "im Dunkeln rumliegenden"
Halbleiters vor (=Gleichgewicht). | |
|
 |
Hier haben wir: - Links p-Typ-Material.
- Rechts n-Typ-Material
Die Lage der Fermienergie zeigt die Dotierung eindeutig an. Außerdem haben wir dasselbe Material links und rechts,
da die Energielücken identisch sind. | |
|
 |
Im Übergangsbereich müssen die Bänder "irgendwie" verbogen sein.
Damit gibt es ein elektrisches Feld im Übergangsbereich und so gut wie keine freien
Ladungsträger. | |
 |
Wie zuvor wandern Elektronen vom n-Si zum p-Si, weil es dort jede
Menge freie Plätze bei tieferen Energien gibt; für Löcher ist es entgegengesetzt. |
|
|
 |
Die ortsfesten ionisierten Dotieratome bleiben zurück; es entsteht eine Bandverbiegung
mit Raumladungszone und elektrischem Feld. | |
 |
Es fließen ständig Elektronen- und Löcherströme ji
von links nach rechts und zurück. | |
|
 |
Im Gleichgewicht gilt aber:
Sj i=0 . | |
| | |
| | |
 |
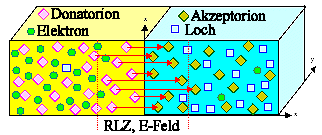
Im Ortsraum sieht es so aus Þ |
|
|
|
 |
Die Weite der RLZ is analog zum Fall der Oberfläche: Proportional zur Wurzel aus
der Differenz der Fermienergien (oder der wirkenden Spannung) und umgekehrt proportional zu einer Art "Mittelwert"
der Dotierkonzentrationen. | |
|
| | | |
 |
Die Ströme habe Namen Þ |
|
Strom der Majoritäten in das jeweils andere Gebiet.
Beispiel: Elektronenstrom vom n-Si
zum p-Si: - Diffusionsstrom, oder
- Rekombinationsstrom , oder
- Durchlaßstrom .
|
Strom der Minoritäten in das jeweils andere Gebiet.
Beispiel: Elektronenstrom vom p-Si
zum n-Si: - Feldstrom , oder
- Driftstrom, oder
- Generationsstrom, oder
- Sperrstrom .
|
|
|
 |
Im Durchlaßbereich einer Diode
, die ein pn-Übergang immer darstellt, fließen die Ladungsträger letztlich per Diffusion
von der hohen zur niedrigen Konzentration (1. Ficksches Gesetz).
Auf der "anderen" Seite sind sie jetzt überzählige
Minoritäten und verschwinden durch Rekombination. |
|
|
 |
Im Sperrbereich einer Diode, die ein pn-Übergang
immer darstellt, fließen die Ladungsträger letztlich per Drift im elektrischen
Feld
der RLZ zur anderen Seite – aber immer nur so viele, wie durch Generation
ersetzt werden können. | |
| |
| | |
|
 |
Die Größe der 4 Teilströme läßt sich bis auf
einen Proportionalitätsfaktor (der sich zu 1 ergibt, wenn man aufwendig rechnet) sofort ableiten: |
|
| jF(L) = |
– e · L· nMin (L)
t | = |
– e · L · (ni)2
NA · t |
| jF(V) = |
– e · L · nMin(V)
t | = |
– e · L · (ni)2
ND · t |
|
| jD = | – jF
| |
im Gleichgewicht,
d.h. für jext=0 |
|
|
|
 |
Der (feldgetriebene) Sperrstrom
jF ist proportional zu: - Einzugsgebiet
des pn-Kontakts= Diffusionslänge
L , weil Minoritäten weit weg von dem pn-Übergang per Rekombination verschwinden, bevor sie
zun "Abhang" (=elektr. Feld der RLZ) kommen und dann unweigerlich "hinunterfallen".
- Generationsrate
G=nmin/t, denn mehr als das, was pro Sekunde generiert
wird, kann pro Sekunde nicht abfließen.
- Ladung
q=±e .
| |
|
 |
Der (diffusionsgetriebene) Durchlaßstrom
jD ist im Gleichgewicht entgegengesetzt gleich groß wie der Sperrstrom, da im Gleichgewicht
( Uext=0) der externe Strom jext=0 ist. |
|
| |
| | |
|
 |
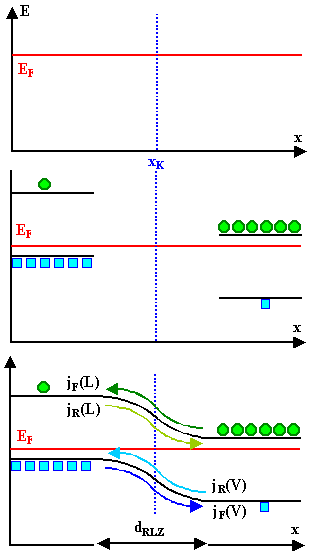
Beim pn-Übergang mit amgelegter Spannung Uext
verschieben sich die Bänder um ±e Uext
. Die Fermienergie ist kein waagrechter Strich mehr ndash; sie ist gar nicht
mehr definiert, denn wir haben, da jetzt Netto-Strom fließt, kein Gleichgewicht
mehr. | |
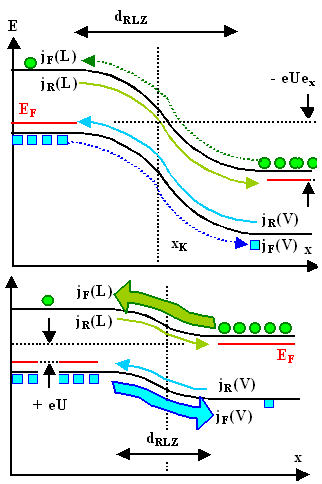
(Hinweis: In dieser Abbildung sind die Teilströme noch englisch beschriftet: Diffusionsstrom=forward
current jF, Feldstrom=reverse current jR) |
|
|
 |
Weit weg vom pn-Übergang hat sich aber nicht viel geändert, dort zeichnen
wir die Bänder wie gewohnt. | |
 |
Was bei den Strömen passiert, ist leicht zu sehen: |
|
|
 |
Nichts beim Sperrstrom. Ladungsträger, die zum "Abhang"
gelangen, fallen runter, egal wie tief es runtergeht. | |
|
 |
Für den Durchlaßstrom hat sich die Energiebarriere, über die er fließen
muss, um ±e|Uext | erhöht oder erniedrigt – je nach Vorzeichen der
angelegten Spannung. Er wird sich dadurch gegenüber dem Durchlaßstrom jD(U
ext=0=– j F) um exp[-eUext/(k BT)]
erniedrigen oder erhöhen: | |
| |
| | |
| |
| jD(U ex ) = |
| jF | · exp( |
+ eUex
kBT |
) |
|
| |
| |
| | |
|
 |
Es ergibt sich sofort die Diodengleichung | |
|
| | |
| | |
| | |
| j(Uex) = |
æ
ç
è |
| jF (L) | + | jF(V) | |
ö
÷
ø | · |
æ
ç
è |
exp( |
eUex
kBT |
) – 1 |
ö
÷
ø |
| | | |
| | |
| | |
| | |
| j (Uex) = |
æ
ç
è |
e · L · nMin (L)
t | + |
e · L · nMin(V)
t | ö
÷
ø
| · |
æ
ç
è |
exp( |
eUex
kBT |
) – 1 |
ö
÷
ø |
|
|
| | |
| | |
 |
Konventionen: Durchlaßstrom ist immer positiv.
- Durchlaßrichtung für + an p-Teil, –
an n-Teil.
| |
|
|
 |
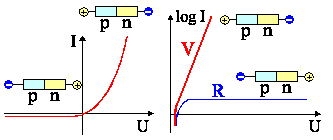
Üblich bei Profis: Diagramm log I vs.
U. | |
|
 |
Maximale Sperrspannung ist begrenzt durch Durchbruch. | |
|
 |
Durchlaßstrom ist begrenzt durch Serienwiderstände. |
|
© H. Föll (MaWi für ET&IT - Script)