 |
In einem ferromagnetischen Material zeigen nach bisheriger Erkenntnis alle magnetischen Moment
in dieselbe Richtung. Damit wäre das Material ein sehr starker Dauermagnet. |
|  |
Ein Stück Eisen oder Nickel, das nur so rumliegt (d. h. sich halbwegs im thermodynamischen Gleichgewicht
befindet), ist aber in der Regel gar nicht aktiv "magnetisch", d. h. kein
Dauermagnet. Es reagiert zwar passiv auf Magnetfelder, die man irgendwie gemacht hat, hat aber selbst kein
Magnetfeld um sich rum. |
 |
Wir müssen wir uns offenbar fragen: Warum
tarnt sich ein ferromagnetisches Material wie Eisen und scheint nach außen unmagnetisch zu sein? Und wie schafft es ein ferromagnetisches Material, mit hochgradiger Ordnung der magnetischen Momente
im Innern, nach außen völlig unmagnetisch zu erscheinen? |
|
 |
Das Warum ist einfach: Ein Stück Eisen oder Nickel, das im thermodynamischen
Gleichgewicht nur so rumliegt, hat per definitionem seine freie Energie G
minimiert. Offenbar gehört zu diesem Minimum zwar ein hoher Grad an Ordnung bei den magnetischen Momenten, aber kein externes Magnetfeld. |
|
 |
Das kann man noch einfach verstehen: Ein Magnetfeld enhält, wie jedes Feld, eine Menge potentielle
Energie. Ein schlaues magnetisches Material kann also den Energieterm U im Ausdruck G=U –
TS deutlich kleiner machen, wenn es sein externes Magnetfeld irgendwie "abschaltet". |
|
 |
Fragt sich jetzt nur wie
? Die naheliegende Antwort, daß die Ausrichtung der einzelnen magnetischen Momente verlorengeht, ist für
Ferro- (etc.-) Magnetica falsch! Das würde zwar die Unordnung und damit die Entropie
S massiv erhöhen, aber bei den paar ferromagnetischen Werkstoffen offenbar zuviel Energie U
kosten. Deswegen gibt es nur einige wenige magnetische Werkstoffe (bei fast allen gewinnt eben doch die Entropie), aber
bei denen gehört die Ausrichtung der magnetischen Momente dann unabdingbar zum Gleichgewicht. |
 |
Die korrekte Antwort auf das "Wie" ist: Es werden Defekte
in der ansonsten perfekten Ausrichtung eingeführt, mit denen das Material dann so in magnetische
Domänen eingeteilt werden kann, daß die Energie des Magnetfelds (und noch ein paar andere Energien) minimiert
werden. |
|
 |
Diese magnetischen Domänen sind auch unter der Bezeichnung Weiss'sche
Bezirke bekannt (benannt nach dem französischen Physiker Pierre-Ernest Weiss). Wir werden hier aber immer nur die
Bezeichnung "Domänen" verwendnen. |
 |
Das nachfolgende Bild macht das generelle Konzept klar. |
| |
|
|
 |
Links ist ein Material mit perfekter Ausrichtung der magnetischen Dipole im gesamten
Volumen gezeigt. Es wäre ein starker Magnet mit einem entsprechenden großen magnetischen Feld im Außenraum. |
|
 |
Rechts sehen wir dasselbe Material, aber jetzt mit magnetischen
Domänen. Die Feldlinien können sich im Inneren schließen; das
externe Feld ist klein. |
|
 |
Ganz rechts ist es im Grunde dieselbe Anordnung, nur mit mehr Domänen. Damit könnte man das externe
Restfeld noch stärker reduzieren. |
 |
Was wird's sein? Nun ja, oben haben wir behauptet, daß Defekte
in der ansonsten perfekten Ausrichtung eingeführt werden. Wo sind sie denn? |
|  |
Klar – zwischen den Domänen müssen Domänenwände
sein, in denen sich die Magnetisierung von der einen zur anderen Richtung ändert. Es gibt davon zwei Sorten; wichtig
ist vor allem die Blochwand. Die Néelwand
spielt nur bei dünnen Schichten eine Rolle |
| |
|
|
 |
In Worten: Bei einer Blochwand dreht die Magnetisierungsrichtung aus der Ebene der M-Vektoren heraus,
bei einer Néelwand dreht sie in dieser Ebene. |
|
 |
Klar ist auch: Eine Domänenwand ist ein zweidimensionaler Defekt in der Orientierung magnetischen
Momente und besitzt deshalb Energie (eV/cm2 ). |
|
 |
Mit mehr Domänen und damit größeren Domänenwandflächen und damit größerer
gesamter Domänenwandenergie
könnte der Kristall zwar sein externes Magnetfeld immer mehr veringern, aber er muss auch den Preis in Form von
Domänenwandenergie bezahlen. Bei irgendeiner Struktur gibt es ein Optimum – eben das Minimum der freien Energie! |
 |
Wenn man dann noch berücksichtigt, daß weitere Energiebeiträge auftauchen,
können sehr komplexe Domänenstrukturen resultieren, die wir
nur sehr schwer berechnen können. Die neben der Energie des externen Felds wichtigsten Energiebeiträge sind:
|
|
 |
"Leichte Richtung": Die Orientierung der
Dipole in einem Kristall möchte immer in der "leichten Richtung"
liegen – z. B. <100> in Fe oder <111> in Ni. Kann sie das nicht, braucht's
zusätzliche Energie. Damit wird die Domänenstruktur in Polykristallen nicht ganz einfach sein können.
|
|
 |
In Richtung der Magnetisierung ändert der Kristall im allgemeinen auch noch seine Dimensionen –
er wird i.a. kürzer, da die Bindung durch die magnetische Interaktion "verstärkt" wird. Magnetisierung
verusacht also Dehnung, und diesen Effekt nennt man Magnetostriktion. Damit kommt
bei ausgerichteten Momenten auch eine elastische Energie ins
Spiel. Als wichtiger Effekt reagiert damit die Magnetisierung auf Verformung und "spürt" das Verzerrungsfeld
um Defekte. Magnetostriktion ist nicht nur wichtig zum Verständnis der Domäneneigenschaften, sondern auch in der
Technik; wir gehen aber nicht weiter darauf ein. |
 |
Domänenstrukturen zu berechnen
ist damit sehr schwer. Das Material selbst aber hat keine Probleme damit, alle Beiträge zu berücksichtigen
– es macht halt schlicht die Struktur mit der kleinsten freien Energie! Das sieht dann beispielsweise so aus: |
| |
|
|
 |
Oben links ist ein Ni-Einkristall gezeigt; die Magnetisierungsrichtungen sind eingezeichnet. Das
ist nicht so furchtbar verschieden von unserem Prinzipbildchen. |
|
 |
Das daneben ist "Trafoeisen", d. h. Fe mit ca. 3 % Si (hauptsächlich zur Verringerung
der Leitfähigkeit). Man erkennt Körner des Polykristalls mit Domänen, die einen "Spagat" machen
zwischen Orientierung in eine leichte Richtung und möglichst kleinem Feld. |
|
 |
Unten links ist eine amorphe GdCo Legierung gezeigt. Leichte Richtungern kann's nicht geben, das
Domänenmuster ist recht hübsch. |
|
 |
Unten rechts zwei Körner des Materials, aus dem die (derzeit) stärksten Permanentmagnete gemacht
werden: "NdFeB" (Eisen-Neodym-Bor) oder genauer gesagt Nd2Fe14B. Sieht ziemlich
komplex aus, ist aber nur ein Ausdruck der Minimierung der freien Energie. Neodym (Nd) gehört zu den seltenen Erden im Periodensystem – eine Materialgruppe,
die derzeit (2011) häufiger in den Schlagzeilen der Medien zu finden ist, da China 95 % der Weltproduktion kontrolliert
und ohne seltene Erden die gesamte "High-Tech"-Produktion in Deutschland und anderen führenden Staaten sofort komplett zusammenbricht.
|
| | |
|
Magnetisierung mit Domänen |
| |
|
 |
Was passiert jetzt, wenn wir an ein magnetisches Material mit einer Gleichgewichtsdomänenstruktur
von außen ein magnetisches Feld anlegen? |
|
 |
Die Domänen, deren Magnetisierung halbwegs in Feldrichtung zeigen, gewinnen
Energie; der Rest wird energetisch mehr oder weniger ungünstig. |
|
 |
Die Minimierung der freien Energie verlangt jetzt, daß die günstig orientierten
Domänen größer werden, die ungünstig orientierten dafür kleiner. |
|
 |
Für große Felder erwarten wir, daß im wesentlichen nur noch eine Domäne
mit Magnetisierung in Feldrichtung vorliegt. |
 |
Das kann im einfachsten Fall nur so aussehen: |
| |
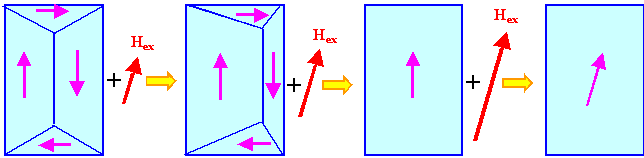 |
| ——— ®
Anwachsendes Feld in roter Pfeilrichtung ———®
|
|
 |
Wie das Ganze real aussieht, ist unten gezeigt. |
| |
|
 |
Wir haben jetzt eine wesentliche Erkenntnis: |
|
 |
Offenbar müssen sich die Domänenwände bewegen,
damit was passieren kann! Damit stellen sich folgende Fragen (mit angedeuteten Antworten):
- Lassen sich Domänenwände einfach verschieben – oder von was hängt's ab? (Þ
Kristallgitterdefekte!).
- Wie schnell geht das verschieben? Steckt möglicherweise hier die Frequenzabhängigkeit der Ferromagnete? ( Þ Nicht sehr schnell; und Ja!
- Geht das vorwärts und rückwärts genau gleich – oder gibt es Hystereseeffekte? (Þ
Nein; und Ja!)
|
|
 |
Den ersten Punkt müssen wir noch etwas genauer betrachten. Über die schon mal kurz
erwähnte Magnetostriktion
spüren Domänenwände Defekte im Kristall und bleiben dann gerne
daran hängen. Sie werden, so sagt man, "gepinnt", d. h.
wie mit einer Nadel (pin) lokal festgesteckt. Zum Losreissen braucht's dann zusätzliche Kraft=höheres externes
Magnetfeld. |
 |
OK – wir gehen nicht in die Details, aber Domänenwände verschieben
ist ein relativ mühsames Geschäft. Es geht weder besonders schnell noch besonders einfach, und die Konsequenzen
sind weitreichend. |
|
 |
Die Frequenzabhängigkeit
der magnetischen Suszeptibilität hängt nur von der Geschwindigkeit ab, mit der sich die Domänenwände
verschieben lassen; sie ist generell recht schlecht. Schon im MHz Bereich wird's i. a. schwierig; nur in kleinen
Spezialstrukturen ist vielleicht noch mal 1 GHz drin. |
|
 |
Bei der Optik geht schon lange gar nichts mehr.
Deshalb schreibt man immer auch nur n=(er)½ und nicht,
wie es eigentlich richtig wäre, n=(er · m
r)½, denn mr ist bei diesen Frequenzen schon längst
=1 |
|
 |
Alles wird ziemlich nichtlinear und wir erhalten Hystereseeffekte.
Wir ausgeprägt sie sind, hängt von der Defektstruktur im Material ab. |
|
 |
Wir brauchen keine "komplexe magnetische Funktion" (obwohl man eine definieren könnte
und das durchaus für spezielle Fälle auch tut). Magnetische Verluste kommen insbesondere auch nicht von einem
Imaginärteil, sondern vom Hystereseeffekt. |
 |
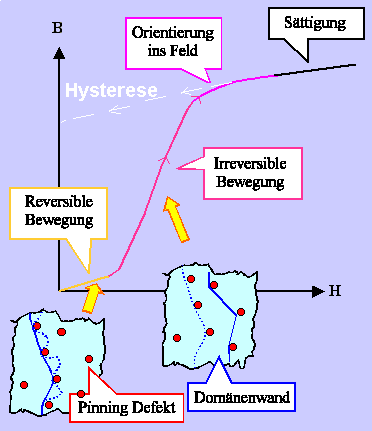
Schauen wir uns nun eine Magnetisierungskurve an; für ein nach außen
zunächst noch unmagnetisches Material. Es sieht etwa so aus: |
| | |
 |
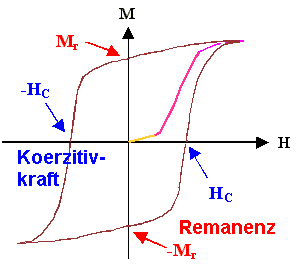 |
Komplette Hystereseschleife mit Definition von
Remanenz und Koerzitivkraft. |
|
|
 |
Für kleine externe Magnetfelder beulen sich die an irgendwelchen Defekten gepinnten Domänenwände
nur etwas in die richtigen Richtungen aus. Die Magnetisierung M (oder der Fluss B) nimmt ungefähr
linear mit dem Feld zu. |
| |
 |
Für größere Feldstärken reissen sich die am höchsten belasteten
Domänenwände los und laufen durch den Kristall, bis sie am nächsten Defekt wieder gepinnt werden. Schaltet
man das Feld jetzt ab, sind sie am neuen Platz gepinnt. Die ganze Chose ist also nicht reversibel, der Ausgangszustand wird
nicht wieder erreicht. |
| |
 |
Bei sehr großen Magnetfeldern gibt es irgenwann nur noch eine
Domäne; die Magnetisierungsrichtung in der Domäne ist aber immer noch in eine leichte
Richtung des Kristall und nicht exakt in Richtung des angelegten Feldes. |
| |
 |
Bei sehr hohem Feld drehen sich die Moment schließlich auch noch in Feldrichtung, und
damit ist Sättigung erreicht. Mehr geht nicht. Ein Bild dazu gibt's in einer Übungsaufgabe
|
| |
 |
Dreht man des Feld wieder zurück, folgt die Magnetisierung einer Hysteresescheifle, die
durch die Zahlenwerte von Remanenz und Koerzitivkraft
halbwegs beschrieben wird. |
| |
| |
 |
Man kann sich jetzt fragen, warum das Material nach Abschalten des Magnetfeldes
nicht immer seine Domänen wieder so justiert, daß das externe Feld Null ist – das braucht's doch zum Minimum
der freien Energie? |
|
 |
Freilich. Aber es braucht manchmal auch ein bißchen Energie, um diesen Zustand einzustellen.
In andern Worten: Unsere hartmagnetischen
Werkstoffe mit ausgeprägter Hysterese bleiben erstmal in einem metastabilen Zustand hängen. Um ins absolute
Minimum zu gelangen, muss man entweder sehr lange warten, oder etwas Energie zuführen. |
|
 |
Bevor wir uns aber den Begriffen "hartmagnetisch"
und "weichmagnetisch
" näher zuwenden, schauen wir uns schnell noch die Thematik " magnetische Verluste"
näher an. |
| |
| |
 |
Zeit für eine Übung |
| |
|
| |
|
| | |
|
© H. Föll (MaWi für ET&IT - Script)