Lösung zur Übung 5.3-1

Eigenschaften der Fermiverteilung

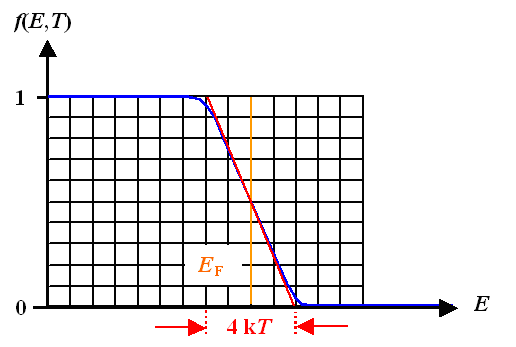
1. Zeige, daß das Aufweichungsintervall der Fermieverteilung in etwa den Wert 4kT hat.
Die Ableitung der Fermieverteilung nach der Quotientenregel ergibt unmittelbar
df(E, T)
dE		   =  – 1
kT		 exp(..)
{exp(..) + 1}2
Für E = EF wird der Exponent = 1 und wir bekommen
 
df(E = EF, T)
dE 		   =  – 1
4kT
Ersetzen wir die Fermiverteilung um EF durch eine Gerade mit der Steigung –(1/4kT), definiert sie gerade ein Aufweichungsintervall von 4kT wie unten gezeigt.
Aufweichungszone der Fermiverteilung
 
2. Zeige, daß für E >> EF die Boltzmannnäherung gilt.
Für E >> EF und (E – EF) >> kT steht im Exponent eine Zahl >> 1
Damit ist exp(E – EF)/kT  >>  1 und die +1 im Nenner kann vernachlässigt werden. Man erhält
f(E >> EF, T)   »   1  
exp(E – EF)/kT		   =   exp– (E – EF)/k T
Das ist die Boltzmannverteilung!
Für welchen Wert E - E F ist die Abweichung der Boltzmann-Näherung von der exakten Formel im Bereich < 10 %? Was folgt daraus?
Mit E - EF = D E haben wir.
exp– DE /kT
  =  1.1  =  1 + exp– DE/kT
    1  
expD E/kT + 1 		        
Man erhält sofort
DE  ³  2.3 kT
Sobald man also energetisch einige kT oberhalb der Fermienergie "sitzt", ist die Boltzmann-Näherung völlig OK.
     

Mit Frame Mit Frame as PDF

gehe zu Übung 2-3-1

© H. Föll (MaWi für ET&IT - Script)