 |
Frage 3: |
|
 |
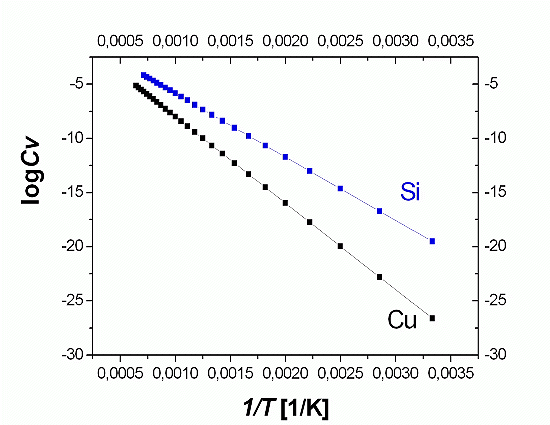
Hier nochmal die Graphik mit einem eingezeichneten Steigungsdreieck |
| |
|
|
 |
Die Steigung ist offenbar so um –5/ 0,000625 = 8000 K–1 |
 |
Aufgetragen haben wir logc = log[exp–(EF/kT
)] = log(e) · ln[exp(–EF/kT)] = –log(e) · (EF/kT
) oder y = –(log(e) · EF/k) · x
. |
|
 |
Man muss hier höllisch aufpassen., ob mand 10-er oder natürlichen Logarithmus
genommen hat! |
|
 |
Damit gilt Steigung = 8000 K–1 = log(e) · EF/k
oder EF = (1/log(e)) ·k · 8000 K–1 = 2,3 · 8000 K–1
· 8,6 · 10–5 eV·K–1 = 1,58 eV |
|
 |
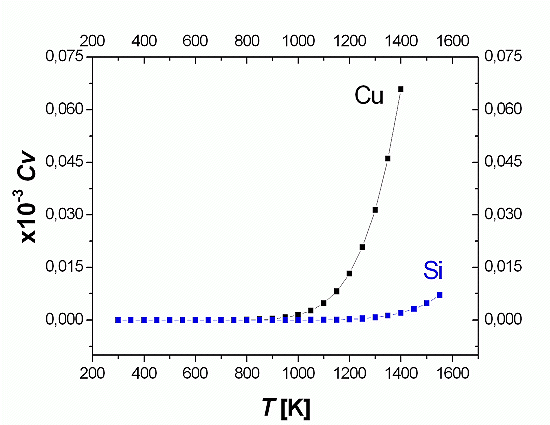
Klar ist auch, dass es besser gewesen wäre, den Maßstab der x-Achse
genauer zu geben (z.B. als mehrstellige Zahl mit 10–3 für die ganze Achse). |
© H. Föll (MaWi für ET&IT - Script)
![]() Übung 4.2-1 Gleichgewichtskonzentration von Leerstellen und Arrhenius Plot
Übung 4.2-1 Gleichgewichtskonzentration von Leerstellen und Arrhenius Plot