Lösungen zur Übung 3.1.1-2

Ebenen und Richtungen im Gitter

Frage 1: Indiziere alle eingezeichneten Richtungen in dem Gitter des gezeigten Kristalls.

Hier ist die korrekte Indizierung:

Nicht vergessen, dass man immer erst den Ursprung der Koordinatensystems, d.h. den Nullpunkt der Basisvektoren in den "Beginn" eines Richtungsvektors legen muß.

Oder eben die Richtung solange verschieben, bis sie durch den Ursprung läuft.

Frage 2: Indiziere die markierten Ebenen im gegebenen Koordinatensystem des Gitters.

Hier ist die korrekte Indizierung:

Wie kommt man auf dieseLösung? Nun gut, einmal langsam zum Mitdenken:

Zuerst verschieben wir den Nullpunkt, so dass er nicht mehr auf der zu indizierenden Ebene liegt. das ist oben rechts schon angedeutet.

Um die Schnittpunkte genau zu bestimmen, betrachten wir jetzt einfach nur die Projektion auf die a₁/a₂ Ebene (mit zwei verschiedenen Ursprüngen). Das reicht bei der ersten Aufgabe aus, da die Schnittpunkte aller Ebenen mit a₃ alle bei ¥ liegen; der dritte Index ist also immer = 0

Es ist jetzt klar, dass man immer dieselben Miller Indizes erhält.

Hier die Lösung der nächsten Aufgabe:

Jetzt noch die Sache mit den Ebenenscharen. Sie zeigt, warum man nicht "kürzen" darf.

Mit Frame

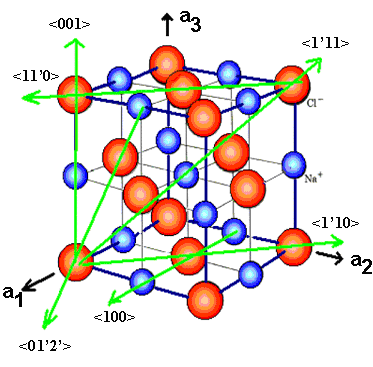
Übung 3.1.1-2 Richtungen im Gitter