2.5 Zusammenfassungen zu Kapitel 2

2.5.1 Merkpunkte zu Kapitel 2 "Bindungen und einige Eigenschaften der Festkörper"

Bindungspotentiale und erste Eigenschaften    
       
Zwischen zwei Ionen gibt es anziehende und abstoßende Kräfte; im Gleichgewichtsabstand r0= Bindungsabstand ist die Summe der Kräfte = 0  
U( r ) = – r
ó
õ
r0 		F (r') · dr'
F = – grad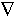[ U(r)]   =   – U(r)

Fx = – U
x		 ,   Fy = – U
y		 ,    Fz = – U
z
Für Ionen ist die anziehende Kraft = Coulombkraft; sie nimmt als Funktion des Abstands r mit r–2 ab.  
Über die abstoßende Kraft wissen wir nur, dass sie bei zu großer Nähe sehr schnell sehr groß wird, d. h. mit einer Funktion wie r–m, m >> 2) anwächst.  
Statt Kräften betrachten wir aber besser das zugehörige Potential U (r), gleich dreidimensional als Funktion des Ortsvektors r .  
Das Potential der Coulombkraft hat also die Funktionalität
UCoulomb µ r–1 		 
         
Aus abstoßendem Potential und anziehendem Potential kann man, falls überhaupt eine Bindung vorliegt, durch (vorzeichenrichtige) Addition immer einen Potentialtopf U(r) konstruieren.  
Bindungspotential
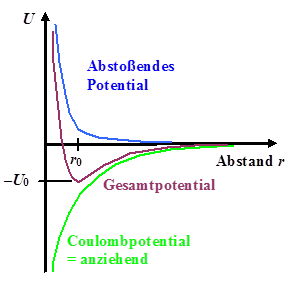Konstruktion Potentialtopf
Das abstoßende Potential wird mit B / r m beschrieben.  
Das anziehende Coulombpotential wird mit –ACou / r beschrieben; mit ACou = (q1 · q2)/(4pe0)  
Falls wir nicht nur die Coulomb Wechslwirkung zwischen zwei isolierten Ionen betrachten, sondern die zwischen einem Ion in einem Ktristall und allen ( ¥ vielen) anderen, muss ACou mit der Madelung-Konstanten a » 1,5 ... 4,5) multipliziert werden.  
Als eine allgemeine Näherungsformel mit A = a · ACou dient dann die Gleichung  
 
UIon( r) =   B 
rm		   –   A 
r 
 
 
Um die Bindungsenergie zu erhalten, muss zur Tiefe des Potentialtopfes U0 noch die Energiebilanz aus Ionisierungsenergie I und Elektronenaffinität A addiert werden, da aus den Atomen zuerst Ionen werden.  
XAtom + I  =  X+Ion + e–
X–Ion + A  =  XAtom + e–
Kleine Ionisierungsenergien liegen im Bereich von 5 eV (Alkali-Metalle), große Elektronenaffinitäten im Bereich 3 eV (Halogene).  
   
Von der Ionenbindung kommt man leicht zu jeder Bindung: sie braucht einen Potentialtopf und kann immer in folgender Form geschrieben werden:
Im Bindungspotential steckt:
  • Struktur des Festkörpers (Kristall, welcher Typ, ...).
  • Elastizitätsmodul E.
  • Thermischer Ausdehnungskoeffizient a .
  • Schwingungsfrequenz der Atome im Kristall.
  • Maximale Bruchfestigkeit.
  • Ungefährer Schmelzpunkt.
   
UBdg(r ) =   B 
rm		   –   A 
rn
 
       
Von den vier Unbekannten A, B, m, n können zwei durch die leicht zu messenden Größen U0 und r0 substituiert werden; n ist manchmal bekannt (s. o.).  
Im Bindungspotential stecken viele wichtige Eigenschaften des zughörigen Kristalls  
     
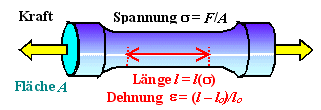
Der Elastizitätsmodul E misst die durch eine mechanische Spannung s verursachte Dehnung e eines Materials.
Zugversuch
Er ist gegeben durch  
   
E  =  1  
r0 		 · d2U 
dr2  
 
     
Bindungstypen und Eigenschaften    
       
Man kann vier Bindungstypen unterscheiden: Ionische, kovalente, Metall- und Sekundärbindungen.  
Edelgaskonfiguration
Treibende Kraft für alle Bindungen ist die Möglichkeit der Energiesenkung durch Annäherung an "abgeschlossenen" Schalen oder Orbitale (Edelgaskonfiguration) plus evtl. daraus folgende Coulombanziehung.  
     
Die anziehenden Kräfte der Ionenbindung sind rein elektrostatisch. Das zugehörige Potential ist das Coulomb-Potential (mit Madelungkonstante).  
Ionenkristalle
Ionenkristalle haben typischerweise starke Bindungen, sind Nichtleiter und durchsichtig, da keine freien Elektronen vorhanden sind.  
   
Merke:
  • Elektrische Leitfähigkeit beruht auf freien, d. h. im Kristall beweglichen Elektronen.
  • Lichtteilchen, d. h. Photonen, interagieren nur mit freien Elektronen
    
       
In kovalenten Bindungen "teilen" sich die Bindungspartner einen Mangel an Elektronen.  
kovalente Bindung im Wassermolekül
Sind die Elektronen in anderen als s-Orbitalen, sind die Bindungen automatisch gerichtet  
Typischerweise starke bis sehr starke Bindungen.  
Typischerweise keine freien Elektronen, d.h. durchsichtige Isolatoren.  
Aber: Halbleiter sind meist kovalent gebunden. Freie Elektronen entstehen durch thermische Energie und Defekte.  
       
In metallischen Bindungen werden überschüssige Elektronen an den Kristall abgegeben.  
Metallbindung
Die positiv geladenen Ionenrümpfe sitzen wie Rosinen im Teig des Elektronengases. Die Bindungsstärke reicht von sehr schwach sein (z. B. Hg, Ga) zu sehr stark (z. B. W, Ta).  
Metall haben also eine Dichte an freien Elektronen in der Größenordnung der Atomdichte.  
Metalle sind leitfähig und undurchsichtig.  
         
Sekundäre Bindungen sind relativ schwach (und ermöglichen damit "das Leben" bei Raumtemperatur).  
SiO2-Bindung
ionisch : kovalent » 50 : 50
gemeinsame Elektronen sind eher beim O
Þ O ist neg. geladen
Wichtig sind Dipol-Dipol-Bindungen (Van-der-Waals-Bindungen) und die Wasserstoffbrückenbindung.  
Im allgemeinen Fall treten Bindungen gemischt auf:  
         
Essenz der Quantentheorie    
       
Für alle Rechnungen sieht das Schema so aus:
  • "Input" ist das Potential U(r).
  • "Output" ist die komplexe Wellenfunktion y(r)
  • plus die (konstante) Gesamtenergie E.
  • Die Verknüpfung von Input und Output leistet die Schrödingergleichung Þ
  
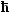–  2
2m		 · y +   (U – E) y =  0
Das Betragsquadrat y · y* · dV gibt die Wahrscheinlichkeit an, das behandelte Teilchen im Volumenelement dV zu finden.  
 
Im allgemeinen gibt es viele (meist ¥ viele Lösungen, die mit Quantenzahlen n, m, ... durchnumeriert werden.  
Potentialtopfmodell eines Atoms
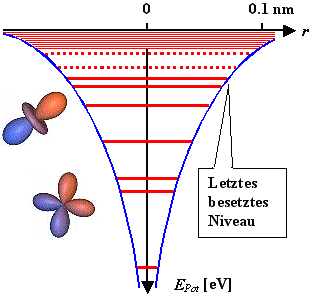Die Ionisierungsenergie I ist im Bild enthalten!
Eine spez. Lösung = ein möglicher Zustand des Systems  
Zu jedem Zustand yn, m, ... gehört eine Energie En, m, ...  
Verschiedene Zustäden können dieselbe Energie haben. Die Energie ist dann bezüglich der zustandsbeschreibenden Quantenzahlen entartet.  
Was man erhält, z. B. für ein Atom, kann wieder in einem Potentialtopfmodell visualisiert werden.  
Gezeigt sind zwei Wellenfunktionen = Zustände, und Energieniveaus aus den zugehörigen E-Werten.  
Welche Lösungen realisiert werden (= welche Zustände besetzt werden), entscheidet
  • die Natur der betrachteten Teilchen sowie
  • die "Temperatur" oder die Einbettung in die "Umwelt" (in der Regel das Prinzip der Minimierung der Energie).
  
 
Es gibt zwei fundamentale Teilchensorten:
  • Bosonen ; mit ganzzahligem Spin; z. B. Protonen, Neutronen, Photonen.
  • Fermionen ; mit halbzahligem Spin; z. B. Elektronen.
  
Elektronen in einem
System können nie
denselben Zustand einnehmen
Für Fermionen gilt das unglaublich wichtige Pauli-Prinzip:  
         
Wichtig ist, was passiert, wenn man aus einelnen Potentialtöpfen für Elektronen einen Kristall macht – durch Überlappung der Einzetöpfe.  
Bändermodell
Das Pauli-Prinzip erzwingt die Aufspaltung von überlappenden Einzelniveaus in Bänder (bei gleichzeitiger Energieabsenkung; sonst keine Bindung!).  
Wie diese Bänder genau aussehen, d.h. wieviele Plätze (= Zustände) sie Elektronen bei der Energie E bieten, entscheidet über die wesentlichen elektronischen Eigenschaften des Materials (Leiter, Halbleiter, Isolator, ...).  
       
 
Fragebogen
All "Multiple Choice"-Fragen zu Kapitel 2
         
Mit Frame Zurueck Weiter als PDF

© H. Föll (MaWi für ET&IT - Script)