|
Solarzellen sind großflächige pn-Übergänge mit einer
(im Jahre 2003) (0.3 - 0.5) µm dicken p-Si-Seite und einer dünnen (<< 1 µm)
n-Si-Schicht. |
|
 |
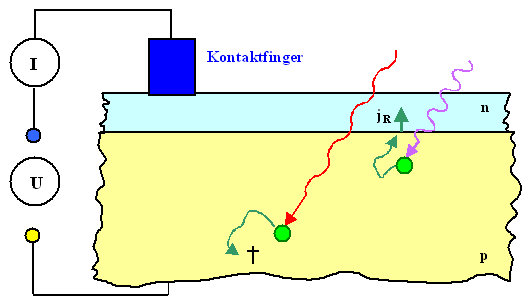
Alle Photonen mit E = h · n > EG
werden im Halbleiter absorbiert wobei ein Elektron-Lochpaar gebildet wird. Alle Photonen mit kleinerer Energie werden nicht
absobiert; ihre Energie geht "verloren". Die photogenerierte Elektronen landen als zusätzliche Minoritätsladungsträger
im Leitungsband des p-Halbleiter. |
|
 |
Die bei kurzwelligen Photonen vorhandene Überschußenergie EG
– h · n geht bei der Thermalisierung der Ladungsträger "verloren",
d.h. macht nur die Solarzelle wärmer. |
|
 |
Damit gibt es ein fundamentales Dilemma: Halbleiter mit kleinem Bandgap abbsorbieren
zwar mehr Photonen, verlieren aber einen Großteil der Überschußenergie; Halbleiter mit großem Bandgap
tun das nicht, aber lassen viele Photonen durch. |
 |
Konsequenz: Relativ zum gegebenen Sonnenspektrum (= wieviel Photonen gibt es bei
welcher Energie) muß es ein optimales Bandgap EGopt geben mit maximalem Wirkungsgrad
h = (Energie aus Solarzelle / Energie im Licht) · 100%. |
|
 |
EGopt liegt bei »
1,5 eV (» GaAs); hmax ist dann » 30 %. Für Si Solarzellen (EG = 1,1 eV) ist der theoretisch
maximale Wirkungsgrad zwangsläufig etwas kleiner und liegt bei » 25%. |
|
 |
Reale Wirkungsgrade sind immer kleiner, 15 % ist für ein kommerzielles Solarzellenmodul
bereits ein sehr guter Wert. Damit ist die Energie"produktion" im Mittel über alles begrenzt auf (ganz grob
/Faustregel) 100 W/m2. |
 |
Ein Blick auf die grundsätzliche Funktionsweise macht klar, warum die Diffusionlänge,
und damit kristalline Perfektion, der Schlüsselparameter zum Erfolg ist (und Si Solarzellen niemals beliebig
billig sein werden). |
| |
|
|
 |
Elektrisch wird die Solarzelle komplett beschrieben durch die Diodengleichung mit einem zusätzlichem
Term für den (Rückwärts) Photostrom |
|
|
| j(Uex) = |
æ
ç
è |
e · L · nMin(L)
t | + |
e · L · nMin(V)
t | ö
÷
ø
| · | æ
ç
è
| exp |
eUex
kT |
– 1 |
ö
÷
ø |
– jr(solar) |
|
|
 |
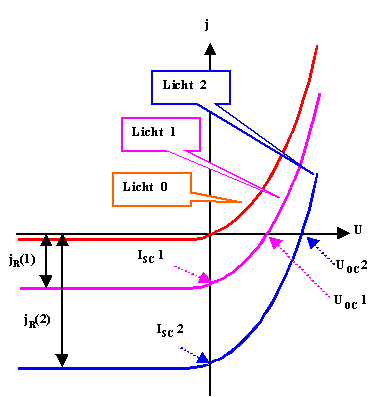
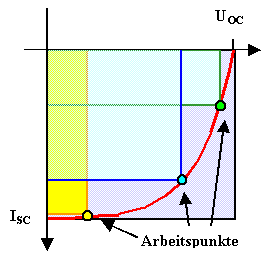
Die graphische Darstellung ist einfach und aufschlußreich: Sie definiert
direkt die Schlüsselparameter Kurzschlußstrom (ISC); Leerlaufspannung (UOC),
Füllfaktor (FF) und optimaler Arbeitspunk (AP). |
|
|
|
| |
|
|
Bipolar Transistor |
| | |
 |
Ein bipolar Transistor ist eine Sequenz aus npn oder pnp-dotiertem
Si, wobei der mittlere Teil (die Basis) sehr dünn sein muß (genauer:
dB << L) |
|
 |
Ein Bild definiert die wichtigstem Terme: |
| |
|
 |
Das Prinzip ist einfach: Die in Vorwärtsrichtung geschaltete Emitter-Basisdiode
injiziert einen großen Löcherstrom vom Emitter in die Basis und einen Elektronenstrom von der Basis in den Emitter. |
|
 |
Da die Basis dünn ist, werden viele der injizierten Löcher bis zur RLZ der
in Sperrichtung geschalteten Basis-Kollektordiode gelangen und dann vom dort herrschenden elektrischen Feld in den Kollektor
"gespült". |
|
 |
Es ist wichtig (und einfach), den "Stromlaufplan" zu verstehen: |
| |
|
 |
Bei Vernachlässigung aller "kleinen" Rückwärtströme
und der Voraussetzung, dass j hR(BK) » j
hF(BE), ergibt sich sofort die Stromverstärkung in einfachster
Weise zu |
| |
| b = |
IK
IB |
= | j
hR(BK)
j eF(BE) |
= | j
hF(BE)
j eF(BE) |
= |
| · |
| = |
NA(E)
ND(B) |
|
|
 |
Damit ist die Herstellung eines verstärkenden Elements zurückgeführt
auf Geometrie ("Mache ein sehr dünne Basis (plus "Drähtchen nach außen)") und ein extremes
Dotierverhältnis! |
|
 |
Mikroelektronik wird möglich! |
| | |
© H. Föll (MaWi 2 Skript)