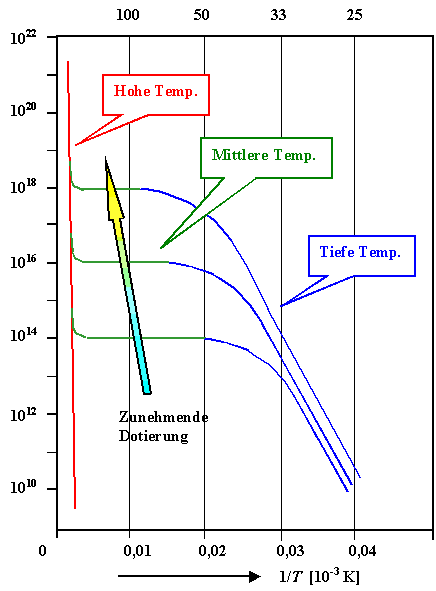
 |
Zunächst eine direkte Gegenüberstellung von den "Prinzipkurven"
aus dem Haupttext und gemessenen Kurven. |
|
 |
Wenn man genügend lange die Skalen umrechnet und berücksichtigt, daß
im Bereich der intrinsischen Leitfähigkeit eine Verschiebung im mm Bereich sofort 100 K Unterschied machen
kann, liegen wir nicht so schlecht. |
|
|
 |
 |
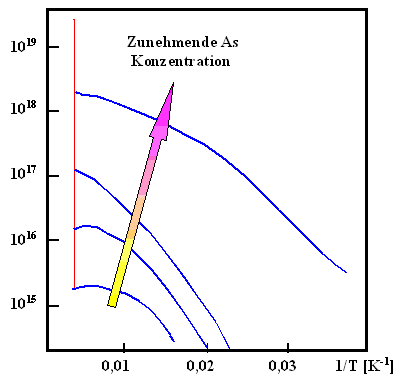| Berechnet |
Gemessen |
|
|
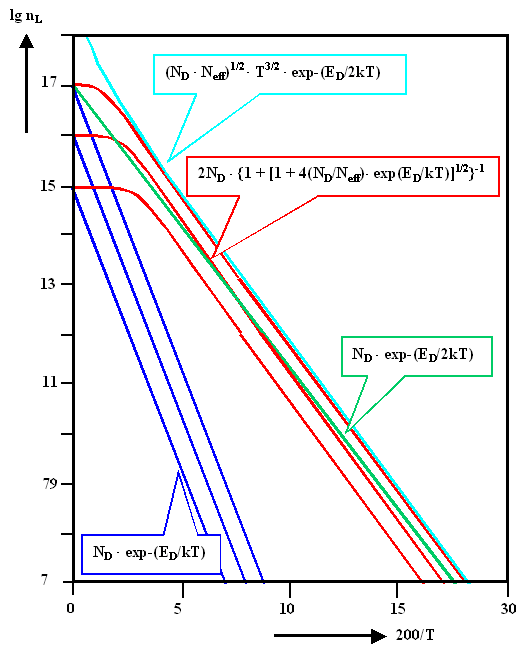
Jetzt die Darstellung einiger Näherungskurven. Als effektive Zustandsdichte
wurde der Wert des freien Elektronengases (Neff = 4,88 · 1015 · T
3/2 cm –3; T in Kelvin einsetzen) verwendet. |
|
|
Zunächst sieht man, daß ein naiver Boltzmannansatz, bei dem man als Energieschwelle
einfach EL – ED nimmt, ganz schön daneben liegt (blaue
Kurven). Das wurde z.B. im "Barrett" gemacht.
|
|
|
Die simple Tieftemperaturnäherung mit (EL – ED)/2kT
im Exponenten (grüne Kurve) liegt bei tiefen Temperaturen in der Steigung nicht schlecht,
verglichen mit den roten "Referenz"kurven, die unsere beste Näherung
repräsentieren. Der Absolutwert ist jedoch kräftig verschoben. |
|
|
Die bessere Tieftemperaturnäherung mit (Neff · ND)½
ist wirklich gut bei tiefen Temperaturen, wird aber kräftig falsch bei mittleren und hohen Temperaturen, wenn der Faktor
T 3/2 beginnt, alles in Richtung ¥ zu ziehen. |
| |
|
|
Man muß also ein bißchen aufpassen, wenn man mit Näherungen arbeitet.
Aber für viele Zwecke sind die einfachen Formeln durchaus ausreichend. |
| | |
© H. Föll (MaWi 2 Skript)
5.2.4 Massenwirkungsgesetz und Ladungstraegerdichten 
Mit Frame