 |
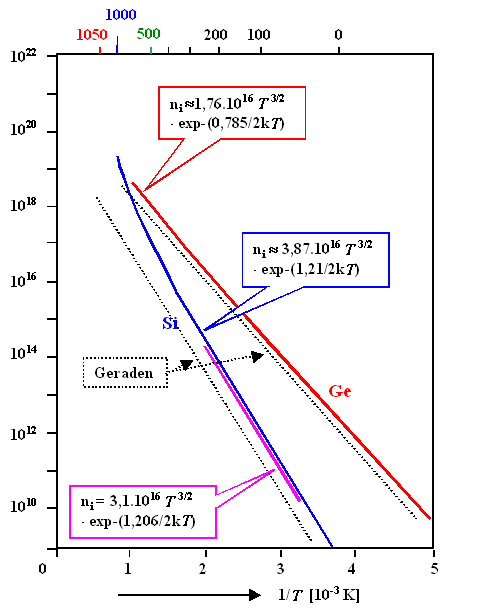
Silizium hat eine Bandlücke von etwa 1,1 eV. Fittet man die gemessene Ladungsträgerdichte an ein T3/2exp –(Eg/2kT)
Gesetz erhält man die folgenden Kurven. |
|
 |
Die Zahlenwerte für den Vorfaktor sind etwas verschieden - je nach dem,
welche Messungen man nimmt und wie man fittet. |
|
|
|
|
 |
Alle Zahlen sind für die Einheit cm –3; T in [K].
Für Si sind zwei Kurven gezeigt - je nach Experiment. Man erkennt, wie wenig der Vorfaktor ausmacht. |
|
 |
Die zwei gestrichelten Geraden verdeutlichen. daß der Faktor T
3/2 keinen großen Einfluß hat. |
|
 |
Die blaue Si - Kurve berücksichtigt sogar die Änderung der Energielücke
mit der Temperatur (z.B weil auch der Gitterparameter sich per Wärmeausdehnung ändert). Sie lautet exakt
|
| |
| ni | = | 3.87 · 1016 · T
3/2 · exp – | 0,605 + DE
kT |
| DE | = |
– 7,1 · 10–10 · |
æ
ç
è | ni
T | ö
÷
ø | 1/2 |
|
|
 |
Die Vorfaktoren sind selbstverständlich nicht
identisch mit dem Zahlenwert, den wir für das freie Elektronengas erhalten haben |
|
 |
Zum Vergleich stehen "theoretische" 4.8 · 1015 · T
3/2 cm –3 und experimentelle ca. 4.5 · 1016 · T
3/2 cm –3 für Si. |
|
 |
Die Zustandsdichte des freien Elektronengases gibt also einen Zahlenwert, der nur eine Größenordnung
"daneben" liegt - nicht schlecht, wenn man bedenkt, wie stark reale Zustandsdichten von der simplen Näherung
abweichen. |
| |
|
© H. Föll (MaWi 2 Skript)
![]() 5.1.2 Lage der Fermienergie im intrinsischen Halbleiter
5.1.2 Lage der Fermienergie im intrinsischen Halbleiter