|
Die Wärmeleitfähigkeit von Metallen
ist wie die elektrische Leitfähigkeit zwar auch elektronisch bedingt, aber: |
|
 |
Bei allen Festkörpern (Metalle inklusive) wird Wärme auch durch Gitterschwingungen
(die wir Phononen nennen) transportiert. Deshalb haben
auch Materialien ohne freie und bewegliche Elektronen noch eine endliche, manchmal sogar
sehr gute Wärmeleitfähigkeit - die beste überhaupt hat z.B. Diamant. |
 |
Die wesentlich Größe ist der Wärmestrom(vektor)
jw, der analog zum elektrischenStrom definiert werden kann, Was dabei fließt ist
reine Energie - als kinetische Energie von Elektronen oder Schwingungsenergie von Atomen. Wir definieren |
| |
| Wärmestromdichte jW = |
Wärmemenge
Fläche · Zeit |
|
|
|
 |
mit [ jw] = J / (m2 · s) = W
/ m2 |
 |
Für einen Wärmestrom benötigt man als treibende
"Kraft" (mit dem Ausdruck "Kraft" hier in symbolischer Bedeutung) einen Temperaturgradienten,
der im eindimensionalen Fall als dT/dx geschrieben werden kann. |
|
 |
Der Wärmestrom, d.h. die transportierte Wärmemenge ist dann proportional zum Temperaturgradienten. |
|
|
|
|
 |
Der Proportionalitätskoeffizient l ([l ] = W
/ m · K) ist die Wärmeleitfähigkeit des Materials. |
 |
Die obige Gleichung ist genausowenig ein Naturgesetz
wie das Ohmsche "Gesetz", sondern beschreibt
eine oft gemachte experimentelle Beobachtung. |
|
 |
Ziel der Festkörperphysik oder Materialwissenschaft ist es, diese Beziehung herzuleiten,
ihre Grenzen aufzuzeigen, und Werte für l zu errechnen. |
 |
Die transportierte Wärmemenge nimmt bei
gleichem Temperaturgefälle mit der Wärmeleitfähigkeit l zu. |
|
 |
Hier einige Zahlenwerte mit typischen Wärmeleitfähigkeiten verschiedener Materialien. |
|
 |
Diamant hat dabei die höchste Wärmeleitfähigkeit aller bekannten Materialien.
Ein echter Diamant fühlt sich deshalb wie Metalle immer kalt an, im Gegensatz zu Glas, da er die Körperwärme
sehr schnell nach "außen" transportiert. |
|
|
Werkstoff |
l [W/m K] |
| Diamant |
2302 |
| Silber |
414 | | Eisen |
72 |
| Quarz |
1.4 | | Styropor |
0.035 |
|
 |
Hier noch ein schnelles Beispiel zum Umgang mit der Wärmeleitfähigkeit
(zum selbst nachrechnen): |
|
 |
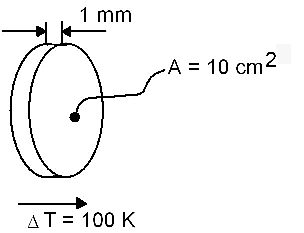
Gegeben ist eine Metallplatte mit den in der Figur gegebenen Dimensionen. Wie schnell wird's
am kalten Ende wärmer? |
| |
|
|
 |
Näherungsweise dauert eine Temperaturerwärmung (zum Abbau des T-Gradienten)
am kalten Ende um 1 K bei einer Eisenplatte 5.1 ms, bei einer Silberplatte jedoch nur 0.6 ms, da die Wärmeleitfähigkeit des Eisens 72 W/(m
K) und die des Silber 414 W/ (m K) beträgt |
|
 |
(Hinweis: Die Temperaturerhöhung ergibt sich aus der zugeführten Wärmemenge
dividiert durch die spezifische Wärme des Materials und dessen Masse). |
| | |
|
1.2.3 Magnetismus |
| | |
 |
Magnetische Eigenschaften von Werkstoffen werden
wesentlich durch den Spin der Elektronen bestimmt. Wir werden sie nicht in dieser Vorlesung behandeln, sondern im 5.
Semester in "Electronic Materials" |
|
 |
Was man aber schon jetzt wissens sollte ist: |
|
 |
Allgemein entsteht durch die Kreisbewegung von elektrischen Ladungen ein magnetisches Moment m,
definiert durch die folgende Gleichung mit der erklärenden Figur: |
| |
| m := I
· A |
| I : | elektrischer Strom | | A: | umkreiste Fläche |
|
|
|
| |
|
|
 |
Die Einheit des magnetischen Momentes ist also: [m] = A
m2. |
|
 |
Auch durch den Spin,
der anschaulich (aber nicht ganz korrekt) als die Eigenrotation des Elektrons aufgefaßt werden kann, wird ein magnetisches
Moment hervorgerufen, welches als Elementarmagnet wirkt. |
|
|
 |
Unter der Magnetisierung
M ([M ] = A / m) versteht man das magnetische Moment pro Volumeneinheit
eines Materials. Die Magnetisierung ist eine weitere elektronische Eigenschaft von Materialien. |
| |
| Magnetisierung M = | magnetisches Moment
Volumen |
|
|
 |
Die Magnetisierung beschreibt also den magnetischen Zustand eines Materials. Es
kann dabei auch ohne eine äußere Einwirkung eine Magnetisierung vorliegen (Wir haben dann einen Permanentmagnet). |
|
 |
Andererseits kann durch die Einwirkung eines äußeren magnetischen Feldes
H0 die Magnetisierung im Inneren eines Körpers verändert werden. Zwischen der Magnetisierung
und einem äußeren Magnetfeld besteht oft ein linearer Zusammenhang. |
| |
|
|
 |
Durch das äußere, magnetisches Feld H0 kommt
es zu einer Veränderung der Richtungen der magnetischen Momente des Festkörpers. Das magnetische Feld im Inneren
des Festkörpers Hi ist dann |
|
|
|
 |
Die durch diese Gleichung (mit derselben Wertigkeit wie das Ohmsche
"Gesetz") eingeführte Materialkonstante c, die magnetische Suszeptibilität, ist ein Maß dafür, wie stark die magnetischen Momente
eines Festkörpers (bzw. Flüssigkeit, Gas) auf ein äußeres magnetisches Feld reagieren. |
|
 |
Alle festen Körper lassen sich an Hand der magnetischen Suszeptibilität
in drei Klassen einteilen: |
| |
|
|
|
| c < 0 : |
Diamagnetische Materialien. |
Das äußere, magnetische Feld wird im Innern abgeschwächt. Die Atome dieser Festkörper haben abgeschlossene
Elektronenschalen und kein nach außen wirkendes magnetisches Moment. Durch das äußere magnetische Feld
wird auf Grund der Lenzschen Regel ein Magnetfeld induziert, was dem äußeren entgegenwirkt und dieses somit abschwächt.
Beispiel: Edelgase |
| c > 0 : |
Paramagnetische Materialien. |
Das äußere magnetische Feld wird im Innern des Festkörpers verstärkt. Die Atome des Festkörpers
besitzen ungepaarte Elektronen und ein permanentes magnetisches Moment. Durch das äußere, magnetische Feld kommt
es zur Ausrichtung der magnetischen Momente des Festkörpers und damit zu einer Verstärkung des magnetischen Feldes
im Innern.
Beispiel: Al, Sauerstoff |
| c >> 0 : |
Ferromagnetische Materialien. |
Es kommt ebenfalls zu einer Verstärkung des äußeren, magnetischen Feldes, die aber erheblich stärker
ist als im paramagnetischen Fall. Auf Grund einer spontanen Magnetisierung
liegen in einem ferromagnetischen Festkörper bereits größere Bereiche mit parallel ausgerichteten magnetischen
Momenten vor (Weiß'sche Bezirke), die durch ein äußeres, magnetisches
Feld ausgerichtet werden können.
Beispiel:
Fe, Co, Ni. |
|
| |
|
|
 |
Ein typischer Wert der Suszeptibilität eines diamagnetischen
Materials ist – 1.4 · 10–6 für Bismut; für ein paramagnetisches Material wie
Sauerstoff (gasförmig) ergibt sich 0.14 · 10–6. |
| |
1.2.4 Dielektrische Eigenschaften |
| | |
 |
Die Einwirkung eines zeitlich konstanten, elektrischen Feldes auf einen Festkörper
mit lokalisierten Elektronen (Isolator) führt zur Erzeugung von elektrischen Dipolen
im Innern. Das ist in der Figur schematisch dargestellt. Auch dielektrische Eigenschaften werden nicht in dieser Vorlesung
behandeln, sondern im 5. Semester in "Electronic
Materials" |
| |
|
 |
Das elektrische Dipolmoment ist definiert als
|
| |
|
|
 |
Mit Q =
elektrische Ladung, l = Abstand der positiven und negativen Ladung. Die Einheit des Dipolmomentes ist
[p] = A · s · m |
 |
Analog zur Magnetisierung definiert man eine größenunabhängige
Polarisation P
|
| |
| P = |
elektrisches Dipolmoment
Volumeneinheit |
|
|
|
 |
mit der Einheit [P] = As/m2. Die Polarisation des Materials
ist - wie wir jetzt schon vermuten - in der Regel proportional zum elektrischen Feld E |
| |
|
|
 |
Dabei ist e0 = Dielektrizitätskonstante
des Vakuum (e
0 = 8.8542 · 10–12 As/Vm), und er
= relative Dielektrizitätskonstante |
 |
Einer hohen Dielektrizitätskonstanten entspricht also eine hohe Polarisierbarkeit
des Mediums. Die Anwendung auf einen Kondensator ist klar: |
|
 |
Die Kapazität eines Kondensator gibt
seine Fähigkeit an, Ladungen zu speichern. Die Kapazität eines Plattenkondensators mit Dielektrikum bestimmt man
nach der Formel |
| |
|
|
 |
Mit F = Fläche der Kondensatorplatte; d = Abstand der Kondensatorplatten |
 |
Ein großes er entspricht also
einer großen Kapazität, die auf eine große Polarisierbarkeit des Dielektrikums im Kondensator schließen
läßt. |
|
 |
Hier einige Werte |
|
|
| Werkstoff |
er
| | Luft |
1 | | Glas
| 2 ... 16 |
| Glimmer | 4 ... 8
| | Wasser |
80.3 |
| Bleitellurid | 400
|
|
© H. Föll (MaWi 2 Skript)