|
Phänomene wie Diffusion, elastische und plastische Verformung oder Bruch
gibt es auch in nichtkristallinen Materialien. Die (atomaren) Mechanismen müssen aber teilweise anders sein, da es
keine Kristallbaufehler wie z.B. Versetzungen geben kann. Wir unterscheiden grob und
ungenau zwischen | |
|
|
 |
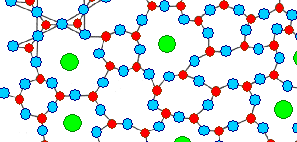
Gläser: "Verhinderte Kristalle" |
|
|
 |
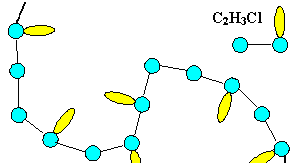
Polymere: Lange Ketten mit fast immer organischen Molekülen
als Kettenglieder = Monomere. |
|
 |
Wir betrachten hier nur (Kohlenstoff) Polymere. Die mögliche Strukturvielfalt
ist gigantisch und ergibt sich aus den möglichen Kombinationen von: |
|
|
 |
Unterschiedliche Möglichkeiten der Verknüpfung der Monomere (ataktisch, syntaktisch,
..). | |
|
 |
Unterschiedliche Kettenlängen und Kettenlängenverteilungen. |
|
|
 |
Viele unterscheidbare Konformationen der Ketten: Von "spaghettiartig"
bis kristallin. | |
|
 |
Mehrere Möglichkeiten Ketten an Knoten zu verknüpfen:
Von simplen "Schlaufen" bis zu kovalenten Bindungen. |
|
|
 |
In weiten Grenzen einstellbare Knotendichte (z.B durch "Vulkanisieren" (= Schwefelbrücken)
beim Kautschuk. | |
|
 |
Mischungen verschiedener Monomere in einer Kette oder Mischungen verschiedener Ketten. |
|
|
| |
|
 |
Trotz der enormen Vielfalt möglicher Polymere, wird man einen "Kunststoff"
fast immer sofort erkennen. Drei Grundtypen werden unterschieden: |
|
|
|
 |
Thermoplaste - werden mit steigender Temperatur weich
oder sogar (zäh)flüssig. Damit leicht formbar. | |
|
 |
Duroplaste - werden mit steigender Temperatur nicht weich
sondern "rauchen ab", d.h. reagieren chemisch und zerstören sich damit selbst. |
|
|
 |
Elastomere - weniger vornehm alles was man mit "Gummiartig"
bezeichnen würde. | |
 |
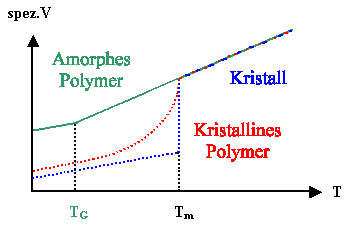
Viele Parameter ändern sich in charakteristischer Weise stetig mit der Temperatur,
z.B. das Volumen | |
|
 |
Ein Schmelzpunkt TM ist nicht gut definiert; wichtiger ist im allgemeinen
die GlastemperaturTG | |
| |
| |
 |
Die beiden Diagramme zeigen die wesentlichen Fakten: |
|
|
|
 |
Alle Polymere verringern um die Glastemperatur herum ihren E-Modul
um mehrere Größenordnungen - falls sie sich nicht vorher schon zersetzen (Duroplaste).
| |
|
 |
Elastomere haben oberhalb der Glastemperatur noch ein mehr oder weniger stark ausgedehntes
"Gummi"-Plateau - je nach Vernetzungsgrad. | |
|
 |
Die Knotendichte bestimmt den Verbeztungsgrad; es gibt
viele Vernetzungsmechanismen. | |
 |
Die wesentlichen Mechanismen sind: |
|
|
 |
Unterhalb Glastemperatur TG:
Langziehen der Bindungen - wie gehabt. Formal als Verbundmaterial behandelbar: "Harte" Fasern (= kovalente
-C-C- Bindungen) in "weicher" Matrix (= Sekundärbindungen zwischen den Seitengruppen). |
|
|
 |
Um GlastemperaturTG: Matrix "schmilzt",
Fasern halten noch, aber werden leicht beweglich. | |
|
 |
Oberhalb GlastemperaturTG: Allmähliches
Verflüssigen über streichkäse- / honigartige Zustände bei wenig Vernetzung, oder "Gummiplateau"
bei höherem Vernetzungsgrad. | |
| | |
| |
 |
Verformungsversuche enthalten jetzt eine dynamische Komponente - die Dehnung wird
u.U, stark zeitabhängig | |
|
|
 |
Man unterscheidet anelastisches und viskoelastiches
Verhalten | |
 |
Das dynamische Verhalten läßt sich mit den zwei Basiselementen "Feder"
und "Stoßdämper" leicht modelieren; diese Elemente sind definiert durch: |
|
|
| |
|
|
|
| |
|
| |
|
|
 |
Dabei sind die Viskosität
e und der E-Modul stark temperaturabhängig. |
|
|
| |
| |
 |
Gummielastizität ist ein reiner Entropieeffekt! |
|
|
|
 |
Im ungedehnten Zustand entspricht die "Zufallsfaltung" einer Kette dem "Random
walk", und damit maximaler Unordnung = Entropie. Der Abstand <r>
zwischen Anfang und Ende entspricht der Diffusionlänge und ist |
|
|
| |
|
|
|
| |
|
| |
| |
 |
Gestreckt wird die Kette ordentlicher, die Entropie nimmt ab, und damit wächst
die freie Enthalpie G. Die rückstellende Kraft F ergibt sich aus nebenstehendem Differentialquotient.
| |
| F | = |
¶ G
¶l |
= – T · |
¶S(r)
¶r |
| |
|
|
|
 |
Die Entropie folgt direkt aus der Verteilung w(x,y,z)DV
der mittleren Abstände zwischen Kettenanfang und Ende, d.h. der Wahrscheinlichkeit des Vorliegens des damit beschriebenen
Makrozustandes. | |
| | |
| |
 |
|
Mit einer Gaussverteilung für w(x,y,z)DV,
einem Übergang von Kräften zu Spannungen sowie Längen zu Dehnungen, und einer simplen Beziehung zwischen
maximaler Kettenlänge und Knotendichte r, erhält man eine verblüffend einfache
Endformel für den E-Modul | |
|
|
 |
Sowohl die Größenordnung (E ist sehr klein), T-Abhängigkeit
und der Zusammenhang mit dem Vernetzungsgrad = Knotendichte wird richtig (wenn auch nur in Näherung) wiedergegeben. |
|
|
 |
Die "Chemie" jedoch spielt keine Rolle! |
|
|
| |
| |
 |
Bei Temperaturen deutlich kleiner oder größer als die Glastemperatur
TG sind die Verhältnisse einfach: | |
|
|
 |
Für T < TG ist das Polymer mehr oder
weniger "spröde"; es bricht nach relativ kleiner Verformung |
|
|
 |
Für T > TG ist das Polymer mehr oder weniger viskos;
es "fließt" wie Streichkäse oder Honig. |
|
 |
Wichtiger sind neue Verformungsarten im Bereich der Glastemperatur, die es praktisch
nur bei Polymeren gibt: | |
 |
Streckung bringt die Ketten permanent
(im Gegensatz zu zum gummiartigem elastischen Verhalten) aus einer geknäuelten in eine gestreckte Konformation. |
|
|
 |
Typisches Beispiel: Manche Folienhüllen oder Bonboneinwicklungen langziehen. |
|
 |
"Crazing" ist eine Mischform zwischen
Sprödbruch und Streckung: Mikrorisse wachsen, aber langsam weil in ihrem Innern noch Ketten gestreckt werden. |
|
|
 |
Typisches Beispiel: Geodreieck oder Lineal biegen. |
|
© H. Föll (MaWi 1 Skript)