 Cu Einkristall (kleine Vergroesserung)" TITLE="click
to enlarge size"> Cu Einkristall (kleine Vergroesserung)" TITLE="click
to enlarge size"> |
 Kristall (hohe Vergroesserung)" TITLE="click to
enlarge size"> Kristall (hohe Vergroesserung)" TITLE="click to
enlarge size"> |
| Das Motto zu Beginn des Hyperskripts gilt auch hier: Auf dem Papier ist es einfach, einen <123> orientierten fcc Einkristall zu verformen; in der Praxis ist es eher problematisch | ||||
| Erstens sind Einkristalle eher selten (oder teuer), und zweitens sind sie so gut wie nie <123> orientiert. Silizium Einkristalle gibt es zwar reichlich und preiswert, aber sie sind immer <100> oder allenfalls noch <111> orientiert. Außerdem kann man sie bei Raumtemperatur gar nicht verformen; dazu müßte man sie kräftig heißmachen (so >800 oC). | ||||
| Also muß man sie sich mühsam selber züchten, oder von jemand, der das kann, schenken lassen (so wie hier; der gezeigte Kristall ist von Herrn Prof. ... der Uni Münster; dort wurde er auch verformt). | ||||
| Hat man dann mit Mühe einen <123> Cu Einkristall etwas langezogen, kommt das nächste Problem: Wie fotografiert man (bei der notwendigen hohen Vergrößerung) die Gleitstufen auf einer stark gekrümmten Oberfläche? | ||||
| Optisch, mit einem normalen Mikroskop, geht das schlicht überhaupt nicht; der Schärfentiefenbereich reicht nicht einmal ansatzweise. | ||||
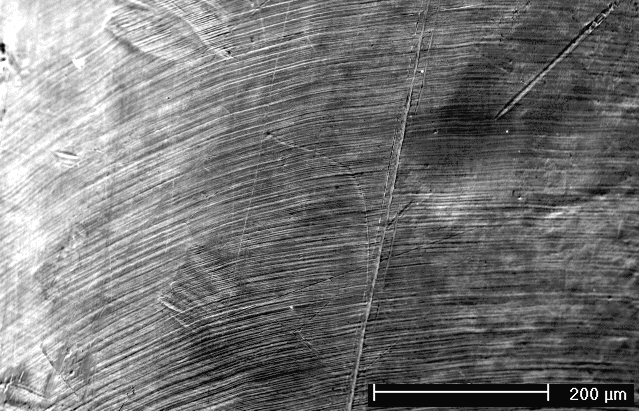
| Wir greifen also zum Rasterelektronenmikroskop (sofern vorhanden). Dort sieht die Oberfläche des jetzt leicht elliptischen Cu Einkristalls bei zwei Vergrößerungsstufen dann so aus (Wir schauen auf den flacheren Teil der Ellipse) | ||||
| ||||
| Alles in allem ist das genau das, was wir als Grundgeometrie erwartet hätten. | ||||
| Gegenüber dem Papierbild gibt es aber noch Zusatzinformation: Der Abstand der Gleitstufen ist einige wenige µm, das hätten wir aus der "Theorie" nicht so ohne weiteres ableiten können. | ||||
| Aus dem mittleren Abstand und der bekannten Gesamtverformung, kann man dann die mittlere Höhe der Gleitstufen errechnen; aus dem Bild ist das nicht direkt entnehmbar. | ||||
![]() 8.2.1 Beobachtungen und Interpretation
8.2.1 Beobachtungen und Interpretation
![]() 7.1.2 Normal- und Scherspannungen
7.1.2 Normal- und Scherspannungen
© H. Föll (MaWi 1 Skript)