8.5 Zusammenfassung / Merkpunkte zu Kapitel 8: Plastische Verformung von Kristallen

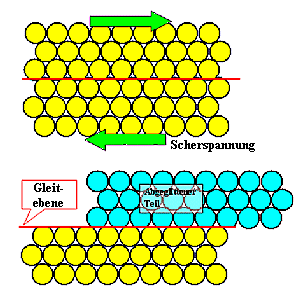
	Plastische Verformung kann immer nur durch blockweises Abgleiten verstanden werden (und nicht etwa durch individuelle Atombewegungen).
		Ein direkter Mechanismus - wie gezeigt - würde Scherspannungen in der Größenordnung von ganz grob 10 % des E- oder G-Moduls benötigen.
		Reale Kristalle verformen sich aber schon plastisch bei Spannungen, die um mehrere Größenordnungen kleiner sind!
		Die entscheidenen Frage ist: Was bestimmt die Fließgrenze Rp, d.h. die minimale mechanische Spannung, ab der plastische Verformung beginnt. Rp ist im übrigen (bis auf einen Zahlenfaktor) so ziemlich dasselbe wie "Härte".
		Konsequenz: Plastische Verformung erfolgt immer durch die (Erzeugung und) Bewegung von Versetzungen.
	Versetzungen sind im Prinzip simple eindimensionale Defekte, trotzdem ist plastische Verformung mit Versetzungen ein sehr komplexer Vorgang.
	Wichtige Eigenschaften von Versetzungen sind:
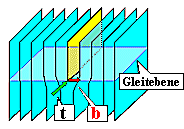
		Charakterisierung durch Burgesvektor b (i.d.R. kleinstmöglicher Translationsvektor des Gitters) und Linienvektor t.
		Versetzungsbewegung erfolgt in der durch b und t aufgespannten Gleitebene. Gleitebenen sind i.d.R. die dichtest gepackten Ebenen des Kristalls. Damit sind die möglichen Versetzungsstrukturen und Verformungen geometrisch eingeschänkt.
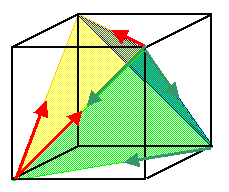
		Beliebige dreidimensionale plastische Verfomung benötigt mindestens 5 Gleitsysteme = kristallographisch verschiedene Kombinationen von Burgersvektor und Gleitebene. In fcc Kristallen gibt es 12 Gleitsysteme (4 Ebenen × je drei b - Vektoren; Bild rechts).
		Die Linienenergie einer Versetzung ist » Gb2 » 5 eV/ |b|; Versetzungen sind damit niemals Gleichgewichtsdefekte. Der Kristall wird deshalb versuchen, die Gesamtlänge aller Versetzungen, d.h. die Versetzungsdichte rVer zu minimieren.
		Versetzungen können nicht im Kristall enden, sondern nur an anderen Defekten und auf Oberflächen / Grenzflächen.
		Scherspannungen in der Gleitbenen üben auf die Versetzung eine Kraft FV senkrecht zur Linienrichtung aus; die Versetzung wird sich bewegen, sobald diese Kraft eine gewisse Mindestgröße überschreitet. Die Kraft pro Längeneinheit ist durch die nebenstehende einfache Formel hinreichend gut gegeben.		FV l  =  t · b
	Damit ist folgender Satz "bewiesen"
		Plastische Verformung erfolgt sobald in den verfügbaren Gleitebenen eine kritische Scherspannung tkrit überschritten wird.
		Diese kritische Scherspannung bestimmt ziemlich unmittelbar die Fließgrenze Rp; sie kann in weiten Grenzen durch geeignete Eingriffe in das Gefüge manipuliert werden.
		Optimierung von tkrit ist die Grundlage der gesamten Metallurgie und damit der Zivilisation.

	Bei einem für Einfachgleitung ortientiertem Einkristall (<123> Orientierung für fcc Gitter) wird bei Erhöhen der Spannung zunächst nur auf einer Gleitebene tkrit überschritten.
	Obwohl nur von geringer praktischer Bedeutung, zeigt der Versuch sehr deutlich was bis zum Bruch geschieht:
		Elastische Verfomung bis zu Rp, d.h. bis zum Erreichen von tkrit auf der "günstig" orientierten Gleitebene.
		"Weiches" Verhalten im Bereich I, da Versetzungen auf der betätigten Gleitebene jetzt laufen können und große plastische Verformung ermöglichen.
		Die blockweise Abgleitung ist (im Mikroskop) gut sichtbar.
		Verfestigung (d.h. "hartes" Verhalten) im Bereich II, weil durch die gestiegene Spannung jetzt auch andere Gleitsysteme betätigt werden, und die Versetzungen sich gegenseitig behindern, d.h. nicht mehr leicht laufen können.
		Entfestigung im Bereich III (Kristall ist wieder "weich"), weil bei den jetzt sehr hohen Spannungen Versetzungen sich von Hindernissen "losreißen" können.
		Schließlich Bruch - auch weil der Kristall jetzt sehr lang, und damit auch viel dünner geworden ist.
	Damit ist auch klar, wie sich Einkristalle verformen, die so orientiert sind dass mehrere Gleitebenen gleichzeitig aktiviert werden (z.B. <100> Orientierung von fcc Gittern):
		Bereich II wird praktisch von Anfang an vorliegen.
	Für Polykristalle, deren Körner "statistisch" orientiert sind, d.h. keine Vorzugsrichtungen haben, werden wir ähnliches Verhalten erwarten.
		Damit haben wir dann "klassische" Spannungs - Dehnungskurven von technischen Materialien im Prinzip verstanden!
		Dass die Realität noch erheblich komplizierter ist, versteht sich dabei von selbst.

	Die kristische Scherspannung tkrit, ab der plastische Verformung einsetzt, kann durch geeignete Maßnahmen in weiten Grenzen manipuliert werden.			tkrit  =  Funktion von: tintrinsisch des Grundmaterial plus: Versetzungsdichte (= Vorgeschichte) Mittlere Korngröße Konzentration an Fremdatomen Konzentration, Art und Größe von Ausscheidungen
		Sie ist zunächst bestimmt durch die intrinsische Fließgrenze ti des (perfekten) Materials - eine Art Materialkonstante.
	Generell gilt: Alle Arten von Gitterdefekten können Versetzungen festhalten("pinnen")
		Wie stark ein Defekt eine Versetzung "pinnt", hängt von Art, Größe und Gestalt des Defektes ab
		Wie stark alle Defekte alle Versetzungen "pinnen", hängt darüberhinaus noch von den Defektkonzentrationen und der Versetzungskonfiguration und -dichte ab.
	Als Mischkristallhärtung bezeichnet man den Anteil tMk, der von atomar gelösten interstitiellen oder substitutionellen Fremdatomen herstammt			tMK = kMK · (cs)½
		Als paradigmatisches Beispiel mag 0.x % Kohlenstoff im sonst recht weichen (Schmiede)eisen dienen: Wir erhalten harten Stahl schon für x < 0.5% !
		Der Zuwachs tMK an kristischer Schubspannung ist i.a. proportional zur Wurzel aus der Kozentration der AF.
	Ausscheidungshärtung arbeitet entsprechend mit Ausscheidungen der zuvor atomar gelösten atomaren Fehlstellen.			tAus  =  2G · b <l>
		Ausscheidungen behindern Versetzungsbewegung zwar i.d.R. weitaus effektiver als atomare Defekte, dafür ist ihre Dichte aber automatisch weitaus geringer
		Der Zuwachs tAus an kristischer Schubspannung ist i.a. proportional zum Kehrwert des mittleren Abstands <l> zwischen den Ausscheidungen
	Verformungs- und Feinkornverfestigung nutzt Versetzungen und Korngrenzen als Hindernisse für die Versetzungsbewegung			tVV  »  0,2 · G · b · (rV)½ tKG  »  kKG <d>½
		Viele Versetzungen erhält man durch plastische Verformung. Vorverformtes Material ist daher härter als jungfräuliches - aber es bricht auch früher! Der Zuwachs tVV ist proportional zur Wurzel aus der Versetzungsdichte rV
		Kleine Körner erhöhen tkrit erheblich um tKG, das umgekehrt proportional zur Wurzel aus mittlerer Korngröße <d> ist.
	Die technische Frage ist nun: Wie stellt an das optimale Gefüge her?
		Und wie erhält man es bei Temperprozessen, insbesondere beim Schweißen?		Schweißen ist ein komplexer Prozeß Die Schweißnaht wird unvermeidlich andere mechanische Eigenschaften haben als das Grundmaterial.
	Denn bei hohen Temperaturen erholt sich das Material, d.h. Defektdichten werden kleiner, und deshalb Körner und Ausscheidungen größer.

	Carbon Steels owe their remarkable properties to the fact that at 996 K there is a phase change of the eutectoid kind:
		Above 996 K: (Non-magnetic) g - phase, fcc lattice; called austenite, able to dissolve up to 2% carbon and still about 0.8 % at 996 K.
		Below 996 K: (Magnetic) a - phase; bcc lattice with hardly any solubility of carbon, called ferrite.
	Even if you would start with a relatively defect free g - phase, the change of lattice type would by necessity introduce many defects and thus lead to some hardening. However, the main hardening effects are due to the need to remove surplus carbon in the a - phase
		Upon slow cooling one obtains pearlite, a mixture of a - Fe and cementite, which is itself an eutectic of a - Fe and Fe3C.
		Upon fast cooling (= quenching) one obtains "lathes" of martensite, a metastable lattice (tetragonal, sort of distorted bcc) with the carbon atoms still dissolved. Martensite is very hard, but brittle
		Tempering below the eutectoid temperature of 996 K will keep part of the hardness, while restoring some ductility: We have "tempered steel", for many years a synonym for the utmost in material strength.
	Adding more alloying element servews to principially distinct goals:
		"Repair" certain problems, e.g. add Mn to compensate for unwanted, but unavoidable S in the mix.
		Produce certain wanted properties, e.g. better corrosion resistance by adding Cr.
	However, each addition infringes on all properties; optimizing can be long and hard work.
	Nevertheless, an incredible richness of steel variants with a huge spectrum of properties is known and produced.
		What can be done with respect to the yield strength RP (proprotional to hardness) is shown in the diagram for the presently ultimate in strength: maraging steels. Note that the yield strength of pure ferrite is about 50 MPa.
	In principle, whatever happens, can be understood by looking at the movement of dislocations.

© H. Föll (MaWi 1 Skript)