8.3.4 Verformungs- und Feinkornverfestigung

Verformungsverfestigung

	Wir haben schon gesehen, daß Versetzungen auf einem Gleitsystem durch Versetzungen anderer Gleitsysteme in ihrer Bewegung behindert werden können.
		Dies gilt ganz allgemein: Versetzungen sind Quellen lokaler elastischer Spannungen und sie reagieren auf Spannungen - das heißt sie "sehen" sich. Egal ob sie sich abstoßen oder anziehen - sie tun sich schwer aneinander vorbei zu kommen.
		Kristalle mit hoher Versetzungsdichte müssen demzufolge eine höhere Fließspannung RP haben als Kristalle mit niedrigen Versetzungsdichten.
		Das ist leicht zu überprüfen: Wir verformen eine Probe bis zu einem bestimmten Punkt und nehmen sie dann als neue Probe. Von der ursprünglichen Probe wissen wir schließlich auch nicht, was damit vorher schon alles passiert ist.
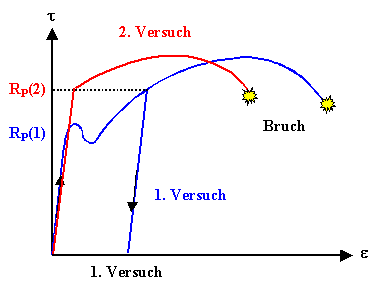
	Die Verformungskurven, die wir erhalten werden, sehen etwa so aus:
		Es klappt also: Proben, die viel Versetzungen enthalten, sind "härter" als welche mit nur wenig Versetzungen.
	Aber Verformungsverfestigung ist tückisch. Sie hängt nicht nur von allen möglichen Parametern ab, sondern kann sich im Laufe der Zeit  g a n z   l a n g s a m  ändern - hier liegt eine der Ursachen für mechanische Alterungsprozesse.
		Theorien müssen sich auf mehr oder weniger einfache Modelle beziehen - hier wird in der harten Forschung viel getan (und viel gestritten).
		Der allgemeinste und stark vereinfachte Ansatz gibt für die notwendige Spannung tVV um Versetzungsbewegung in Anwesenheit anderer Versetzungen aufrecht zu erhalten
		tVV  »  0,2 · G · b · (rV)½
		Mit G = Schermodul, b = Burgervektor; rV ist die Versetzungsdichte.
	Verformungsverfestigung ist uns allen geläufig. Wer hat nicht schon eine Büroklammer so lange hin-und-her gebogen, bis sie bricht.
		Das ist das obige Experiment - nur daß wir nicht ziehen, sondern biegen, also mehrachsige Spannungen bemühen.
	Die Vorgänge bei sehr hohen Versetzungsdichten werden maßlos kompliziert - früher oder später erfolgt der Bruch.

	Feinkornhärtung
	Bisher haben wir nicht berücksichtigt, daß nahezu alle reale Strukturmaterialien Polykristalle sind. Die Frage ist also: Wie überträgt sich die Verformung in einem Korn auf das Nachbarkorn?
		Können Versetzungen durch mehrere Körner durchlaufen? Im Prinzip nicht! Die Zeichnung zeigt warum
	Der Wechsel von einer Gleitebene zu einer anderen über die Korngrenze hinweg ist nicht möglich. Was allenfalls geschieht ist, daß eine Versetzung an der Korngenze absorbiert wird, und eine neue Versetzung auf der anderen Seite emittiert wird
		Verformung erfolgt jetzt so, daß jedes Korn für sich auf die in seinen Gleitsystemen vorliegende Spannung reagiert: d.h. jedes Korn verformt sich - im Prinzip - individuell.
		Da die Körner bald nicht mehr zusammenpassen würden, treten an den Korngrenzen große Spannungen auf, die sich den äußeren Spannungen überlagern und zusätzlich Verformung bewirken, die den Zusammenhalt der Körner ermöglicht.
	Letztlich sind Korngrenzen sowohl sehr effektive Hindernisse für Versetzungen, als auch effektive Quellen. In jedem Fall wird eine zusätzliche Spannung tKG benötigt, um Verformung des ganzen Kristalls zu gewährleisten.
		In einer simplen Näherung, der Hall - Petsch - Beziehung, gilt .
		tKG  »  kKG <d>½
		Mit kKG = Materialkonstante und <d> = mittlere Korngröße.
		Ein feinkörniges Material ist also "härter" als ein grobkörniges.
	Die Spannungs - Dehnungskurven von Polykristallen sehen naturgemäß ganz anders aus als die von Einkristallen.
		Der Beginn der plastischen Verformung ist nicht sauber definiert - die kritische Fließspannung ist in einigen "günstig" orientierten Körnern früher erreicht als in anderen.
		Die Versetzungsbewegung ist durch Korngrenzen von Anfang an behindert - es gibt keinen "weichen" Bereich I wie bei Einkristallen. Wir erhalten die typischen Verformungsdiagramme realer Materialien.

© H. Föll (MaWi 1 Skript)