|
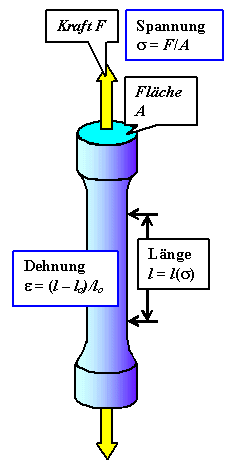
Der Zugversuch ergibt eineFülle von Materialeigenschaften: |
|
|
|
 |
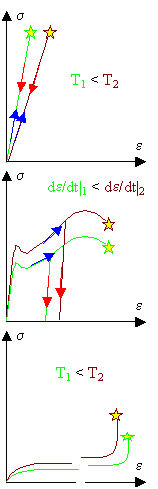
Unterscheidung spröde - duktil - gummiartig usw.; und damit auch elastische
- plastische Verformung. | |
|
 |
Zahlenwerte für E-Modul (E = ds/de); Fließgrenze Rp, max. Zugfestigleit RM,
Bruchdehnung und Spannung, Zähigkeit (Fläche unter s - e
Kurve) als Funktion der Temperatur T und der Verformungsgeschwindigkeit de/dt. |
|
 |
Mechanismen dazu indirekt bestimmbar: |
|
|
 |
Elastizität aus Änderung Bindungsabstände
(alle Kristalle, ...). Maximale Dehnung wenige % oder kleiner. |
|
|
 |
Gumimielastizität: Maximale Dehnung 100 % und mehr
Þ Reiner Entropieeffekt! |
|
|
 |
Plastische Verformung: Erzeugung und Bewegung von Versetzungen. |
|
|
| |
|
 |
Auf beliebigen Ebenen im Probekörper steht die wirkende Kraft nicht senkrecht
auf der betrachteten Ebene, deshalb: | |
|
|
 |
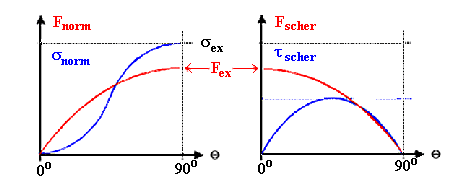
Zerlegung der Spannung in Normalspannungen (s) und Scherspannungen
(t). | |
|
 |
Spannungsverläufe (blau) als Funktion des Ebenenwinkels
Q). sind nicht mehr ähnlich dem Kraftverlauf (rot). |
|
|
 |
Scherspannungen bestimmen die plastische Verformung! |
|
|
| |
| |
 |
Spezielle elastische Verformungen werden mit passenden elastischen Modulen beschrieben |
|
| G = |
E
2(1 + n) |
» 0,4 E (für n » 0,3) |
| K = |
E
3(1 – 2n) |
» 0,8 E (für
n » 0,3) |
|
|
|
 |
Einachsiger Zug (und Druck): E-Modul und Querkontraktionszahl
n » 0.2 .... 0.5 |
|
|
 |
Reine Scherung: Schermodul G |
|
|
 |
Allseitiger Druck: Kompressionsmodul K |
|
|
 |
Benötigt werden in isotropen homogenen Materialien aber immer nur 2 elastische
Module! Ein beliebiger Modul ist immer durch zwei andere darstellbar. |
|
| |
| |
| |
 |
Elastisches Verhalten von Verbundwerkstoffen (Typisch: Hartes Material (z.B. Fasern)
mit EF in weicher Matrix mit EM) ist leicht eingrenzbar: |
|
|
| |
 |
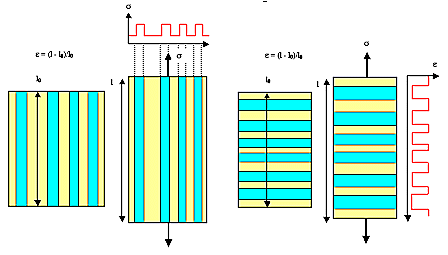
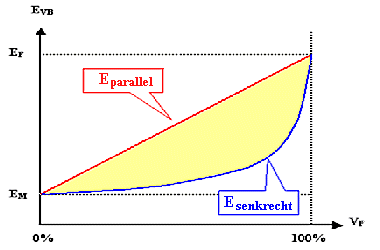
Extremfälle: "Harte" gleichförmig verteilte Fasern mit Volumenanteil VF
senkrecht oder parallel zur Zugrichtung ergibt Extremwerte für den effektiven E-Modul EVB
des Verbundwerkstoffs : Epa und Ese. |
|
| |
| |
| |
| | |
Epa = EF · VF + EM · (1 – VF)
| |
|
| |
|
 |
Entspricht Reihen- bzw. Parallelschaltung von Widerständen (oder Kondensatoren,
oder Mischung von Dielektrizitätskonstanten, oder ...). |
| |
|
 |
Analogie ist weitgehend: Elektrische / mech. Spannung (= Ursache) produziert Wirkung = Dehnung
/ Strom proportional zur Ursache. E bzw. Widerstand R sind Proportionalitätsfaktoren. |
| |
 |
|
Die beiden Extremfälle im EVB - VF Diagramm grenzen
alle möglichen Fälle der Verteilung von hartem Material in weicher Matrix
ein! | | |
| | |
| |
 |
Ein beliebiger Körper verformt sich elastisch unter dem Einfluß beliebiger
Kräfte. Wir beschreiben den Vorgang: |
|
|
|
 |
Aus einem kubischen Volumenelement dV am Punkt r
wird im allgemeinsten Fall ein "geschertes" Parallelepiped. |
|
|
 |
Analogie: Aus einem kubischen Gitter wird ein triklines. |
|
 |
Dazu muß auf jede Fläche des Kubus eine beliebige Spannung wirken können,
die wir in eine Normal- und zwei Scherspannungen zerlegen können: Þ |
|
|
 |
Die "Buchhaltung" erfolgt durch zwei Indizes: Der erste gibt die Ebene an ("i"
für die Ebene senkrecht zu xi), der zweite die Richtung ("j" für xj
Richtung). | |
|
| |
| |
 |
Anordnung der sij und tij
in Matrixform ergibt einen Tensor. Þ |
|
| sij(x,y,z) = |
æ
ç
è |
s11 t12
t13
t21 s22 t23
t31 t32 s33 |
ö
÷
ø |
| si j = s–i
–j | |
| ti j = tj i |
|
|
|
 |
Da unser dV - Würfel sich weder bewegen noch drehen soll, sind nur 6
Komponenten unabhängig. | |
| | |
| |
 |
Tensoren sind Weiterführungen von Vektoren; der Spannungstensor ist ein Tensor
2. Stufe. | |
F = 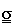 · A · A |
| Fx = sxx · Ax
+ sxy · Ay + sxz
· Az |
| Fy = syx · Ax
+ syy · Ay + syz
· Az |
| Fz = szx · Ax
+ szy · Az + szz
· Az |
|
|
|
 |
Skalare = Tensoren 0. Stufe
Vektoren = Tensoren 1. Stufe (1 Unterstrich)
Spannungen, Dehnungen = Tensoren 2. Stufe (2 Unterstriche)
(E-Modul = Tensor 4. Stufe). |
|
|
 |
Tensoren 2. Stufe verknüpfen Vektorfelder, so dass ein lokaler Vektor, z.B. ein
lokaler Oberflächennormalenvektor A durch Multiplikation mit dem Tensor in einen anderen Vektor
transformiert wird; im Beispiel in die auf die Oberfläche wirkende Kraft F. Þ |
|
|
 |
Der einfachst mögliche Fall einer solchen Verknüpfung ist, dass jede Komponenten
des Kraftvektors von jeder Komponente des Oberflächennormalenvektors abhängt: |
|
|
| |
| |
 |
Die Verknüpfung von Spannungstensor
sij und dem zugehörigen Dehnungstensor
eij braucht im allgemeinsten Fall jetzt einen Tensor 4. Stufe
mit 81 Komponenten; die cijkl
heißen elastische Koeffizienten. Þ |
|
| s11 = |
c11 11 · e11 + c11
12 · e12 + c11 13 · e13
+ c11 21 · e21 + c11 22 · e22
+ c11 23 · s23
+ c11 31 · e31 + c11 32 · e32 + c11
33 · e33 |
| s12 = |
c12 11 · e11 + ....
| | | ........... |
|
|
 |
Mit Symmetrieüberlegungen läßt sich (für die hier immer unterstellten
Einkristalle) die Zahl der elastischen Koeffizienten reduzieren: |
|
|
 |
Im "schlimmstmöglichen" Fall (trikline
Symmetrie) werden 21 elastische Koeffizienten gebraucht. |
|
|
 |
Im einfachsten Fall (kubische Gitter), reichen 2
- daraus lassen sich dann unsere altbekannte elastische Module wie E, n, G
oder K ableiten. | |
|
 |
Der einfachste Fall gilt auch für beliebige isotrope homogene Materialien, z.B. für alle Polykristalle mit "kleinen" willkürlich
orientierten Körnern oder für isotrope amorphe Materialien - und damit für die gebräuchlisten technischen Werkstoffe. | |
|
 |
Speziellen Spannungszuständen entsprechen "einfache" Tensoren. Þ |
|
|
| |
| |
 |
Für einen gegebenen Tensor läßt sich durch eine geeignete Koordinatenstranformation
immer ein Koordinatensystem finden, bei dem alle Nichtdiagonalelemente = 0 sind.
Þ | |
| sij(x,y,z) = |
æ
ç
è |
s1 0 0
0 s2 0
0 0 s3 |
ö
÷
ø |
|
|
|
 |
Dieses KO-System heißt Hauptachsensystem. |
|
|
 |
Tensoren werden, soweit möglich, immer im Hauptachsensystem notiert. |
|
|
 |
Die verbliebenen Normalspannungen werden dann nur mit einem Index geschrieben und der Größe
nach geordnet. | |
| | |
| |
 |
Die maximale Scherspannung
tmax die dann auftreten kann, ist gegeben durch die nebenstehende Formel. Þ | |
|
|
 |
Die Ebenen mit maximaler Scherspannung liegen unter 45o
zu den Ebenen auf denen s1 und s3
wirken. | |
 |
Bedeutung: | |
|
 |
Die maximal möglichen Scherspannungen bestimmen das Auftreten von plastischer
Verformung | |
|
 |
Die maximale Nornalspannung s1 bestimmt das Auftreten
von Bruch. | |
| | |
| |
 |
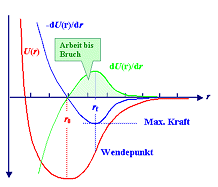
Bruch tritt spätestens dann auf, wenn durch elastische Verformung gegen die
Bindungskräfte soviel Arbeit geleistet wurde, dass die Bindungsenergie übertroffen wird. |
|
 |
| smax » |
æ
ç
è |
E · g
r0 |
ö
÷
ø | 1/2 |
|
|
|
 |
Nach dem Bruch steckt die zugeführte Energie in der Oberflächenenergie
g · A der neugeschaffenen zwei Oberflächen
A. | |
|
 |
Mit diversen Näherungen und Tricks erhält man für die maximale (einachsige
Zug)spannung smax, die ein Material aushält bevor es bricht, die nebenstehende
Beziehung. | |
|
 |
Ein Material ist also umso fester, falls es einen großen E-Modul und eine
große Oberflächenenergie hat. Außerdem sollte der Bindungsabstand r0 klein sein. |
|
 |
Diese Betrachtung liefert aber nur eine absolute Höchstgrenze.
In realen spröden Materialien tritt Bruch i.d.R. schon bei viel kleineren Spannungen
auf. | |
|
 |
In duktilen Materialen erfolgt schon lange vor Erreichen der Bruchspannung plastische Verformung,
dadurch werden die Spannungen angebaut und die Bruchspannung kann nicht (sofort) erreicht werden. Falls die Spannung aufrecht
erhalten wird, wird Bruch aber früher oder später weit unterhalb der theoretischen Grenze erfolgen. |
|
|
| |
| |
 |
Auch reale sprödeMaterialien brechen bei kleineren Spannungen als der theoretischen
Grenze, weil sie Defekte enthalten, die "Mikrorisse" genannt werden. |
|
|
|
 |
Das Konzept der Mikrorisse ist auf jedes Material anwendbar (nicht nur auf Kristalle); in
Kristallen kann ein Mikroriss auch eine Versetzungsaufstauung oder ein Leerstellenagglomerat sein. |
|
 |
Um einen Mikroriss herum sind die lokalen Spannungen anders als im soliden Material,
insbesondere an den Enden können sie sehr hoch werden. | |
|
 |
Andererseits werden im Volumen um den Mikroriss herum die Spannungen schwach sein - das Material
ist dort ja schon "gerissen". | |
|
 |
Eine Vergrößerung der Mikrorissfläche um die Fläche dA
führt demnach einerseits zu Energiegewinn dPRiss, weil um den Riss herum Spannungen, und damit
Energie abgebaut wird, andererseits zu einer Energieerhöhung dPOb durch die neugebildete Oberfläche. |
|
|
| |
| |
 |
Das Bruchkriterium ist dann einfach Nettoenergiegewinn, d.h: Þ |
|
|
| |
| |
 |
Eine simple Näherung (mit c = lineare Ausdehnung des Risses)
ergibt: | |
| s |
> |
æ
ç
è |
8E · g
p · c | ö
÷
ø
| 1/2 |
|
|
|
 |
Aufwendigere Rechnungen ändern nur den Faktor 8 etwas. |
|
|
 |
Nach wie vor ist die maximale Bruchspannung proportional zur Wurzel aus E und
g, aber statt des Bindungsabstandes r0 geht jetzt die Mikrorissgröße ein. | |
 |
Damit können schon kleinste, praktisch nicht nachweisbare Risse im nm
Bereich die Bruchfestigkeit eines Materials erheblich verkleinern! |
|
© H. Föll (MaWi 1 Skript)