|
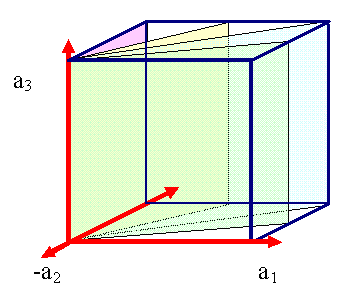
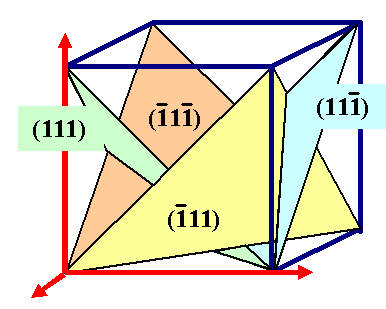
Indiziere die markierten Ebenen und Ebenenscharen im gegebenen
Koordinatensystem |
 |
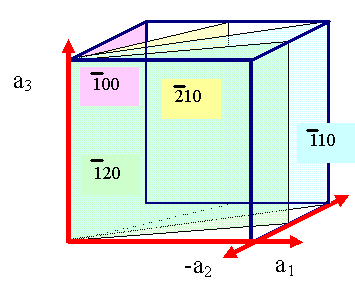
Hier ist die korrekte Indizierung: |
| |
|
 |
Wie kommt man auf dieseLösung? Nun gut, einmal langsam zum Mitdenken: |
|
 |
Zuerst verschieben wir den
Nullpunkt, so dass er nicht mehr auf der zu indizierenden Ebene liegt. das ist oben rechts schon angedeutet. |
|
 |
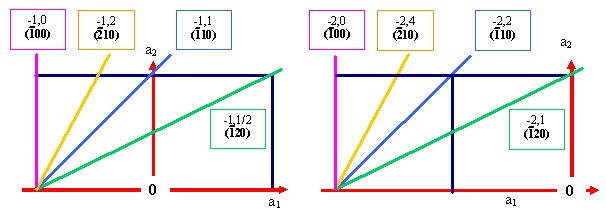
Um die Schnittpunkte genau zu bestimmen, betrachten wir jetzt einfach nur die
Projektion auf die a1/a2 Ebene (mit zwei verschiedenen Ursprüngen). Das reicht bei der
ersten Aufgabe aus, da die Schnittpunkte aller Ebenen mit a3 alle bei ¥
liegen; der dritte Index ist also immer = 0 |
| |
|
|
 |
Es ist jetzt klar, dass man immer dieselben Miller Indizes erhält. |
 |
Hier die Lösung der nächsten Aufgabe: |
| |
|
 |
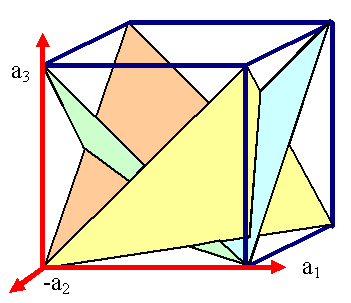
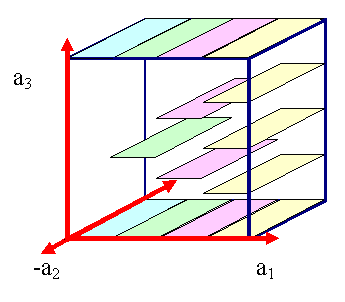
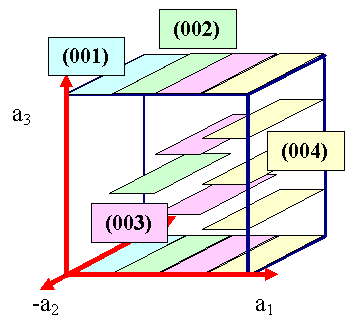
Jetzt noch die Sache mit den Ebenenscharen |
| |
|
 |
Woher weiß man eigentlich, wenn nur eine Ebene eingezeichnet isr, welche
der ¥ vielen möglichen Ebenenscharen gemeint ist? |
|
 |
Einfach: Man weiß es nicht und nimmt automatisch
die kleinstmöglichen Integers als Miller Indizes, das heißt man "kürzt"
im Zweifelsfall. |
|
 |
Das ist aber nur zulässig, wenn es nicht
drauf ankommt, welche Schar genau man anspricht. Sobald wir mit Miller Indizes rechnen
(bei der Beugung von Wellen am Kristall), kommt es sehr wohl darauf an, ob z.B. die {111} oder die {222} Ebenen
involviert sind! |
| |
|
© H. Föll (MaWi 1 Skript)