 |
Ein Kristall hat eine regelmäßige (dreidimensionale - periodische)
Struktur. | |
Kristall = Gitter + Basis
|
|
|
 |
Ein Kristall besteht immer aus (mathematischem Punkt-) Gitter
und (physikalischer) Basis | |
| |
| |
|
|
 |
Das Punktgitter ist vollständig durch einen Satz dreier Vektoren ai
beschrieben; jedem Gitterpunkt kann ein Translationsvektor
T zugeordnet werden | |
| T | = |
u · a1 + v · a2 + w · a3
|
|
|
|
 |
Die Basis ist i.a. ein Atom oder ein Molekül, dabei sind der Komplexität keine Grenzen
gesetzt. | |
|
| |
| |
 |
Ein Gitter kann noch verschiedene Grade an Symmetrie
aufweisen: Neben der immer vorhandenenTranslationssymmetrie auch Rotations-, Spiegel- und Inversionssymmetrien. |
|
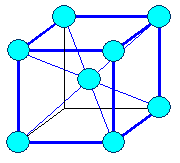
kubisch-raumzentriert
bcc |
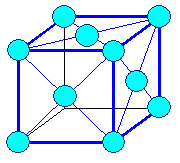
kubisch-flächenzentriert
fcc |
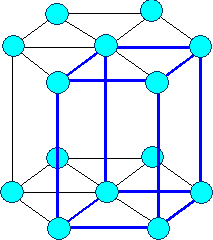
Hexagonal
hcp |
|
|
 |
Je nach dem "Grad" der Symmetrie kann man genau 14 verschiedene "Bravais"-Gitter
unterscheiden. | |
|
 |
Drei davon sind besonders wichtig: fcc, bcc, und hcp. |
|
 |
Die Längen der Basisvektoren der Bravaisgitter heißen die Gitterkonstanten des Gitters. | |
| | |
| |
|
 |
Richtungen werden in einem Koordinatensystem mit den drei Achsen des Bravaisgitters
als kleinstmögliches ganzzahliges Tripel in eckigen Klammern beschrieben
| |
| <uvw> |
Gesamtheit aller kristallographisch
gleichwertigen Richtungen |
| [uvw] |
Spezifische Richtung |
|
|
|
 |
Negative Indizes werden durch einen (in HTML nicht direkt darstellbaren) Überstrich
markiert. | |
Merke:
Allgemeine Indizierung
hat Klammern
mit "Spitzen". |
|
 |
Ebenen werden durch ein ganzzahliges Zahkentripel beschrieben und in runde Klammern gesetzt. | |
|
 |
Die Indizes {hkl} sind dabei die reziproken (und ganzzahlig gemachten) Schnittpunkte
der betrachteten Ebenen mit den Bravaisgitter - Koordinatenachsen. |
|
| {hkl} |
Gesamtheit aller kristallographisch
gleichwertigen Ebenen
| | (hkl) |
Spezifische Ebene |
|
|
 |
Es gibt zahlreiche Fallstricke und Konfusionmöglichkeiten! |
|
Für kubische Gitter gilt:
[hkl] steht senkrecht auf (hkl)
| dhkl = |
a
(h2 + k2 + l2)1/2 |
|
|
|
 |
Die so definierten Miller-Indizes sind aber außerordeentlich
nützlich, da man mit ihnen rechnen kann! |
|
|
 |
Unmittelbar erhält man aus den Miller Indizes für kubische
Gitter den Abstand dhkl zweier Ebenen aus der Schar (hkl) für die Gitterkonstanten
a. | |
| | |
| |
|
 |
Ungefähr 95% aller Elementkristalle haben ein fcc, bcc,
oder hcp Gitter | |
| fcc = "face centred cubic": |
Au, Ag, Al, Fe(T > 720 oC), Ni, ...;
Si, Ge, C(Diamant), ... |
| bcc = "body centered cubic": | Cs, Cr, K, Fe(RT), Ta, V, W, |
| hcp = "hexagonally close packed": | Co, Cd, Mg, Zn, ..; C(Graphit), ... |
|
|
 |
Auch bei Elementkristallen kann dei Basis aus mehreren Atomen bestehen! |
|
|
 |
Wichtiges Beispiel: C(Diamant), Si, Ge: fcc mit 2 Atomen
in der Basis. | |
| | |
| |
|
 |
Wichtige Kenngrößen: |
| |
|
 |
- Koordinationszahl KZ = Zahl nächster Nachbarn
- Packungsdichte PD
- Zahl Atome pro EZ
|
|
| Gittertyp |
fcc | bcc |
hcp |
| KZ | 12 |
8 | 12 |
Atome
pro EZ |
4 | 2 |
2 |
| PD |
0,74 |
0,68 |
0,74 |
| Für 1 - atomige Basis |
|
|
 |
Ein Element kann mehrere metastabile und stabile (als Funktion der Temperatur) Gittertypen
haben | |
 |
Das fcc und hcp Gitter sind Varianten einer Kugelpackung mit gleicher und maximaler Packungsdichte. Die Stapelfolge ist: |
|
|
 |
- ABABA... auf der Basisebene für hcp
- ABCABCA... auf der {111} Ebene für fcc
|
|
|
 |
Dichteste Kugelpackungen sind bei ungerichteten Bindungen grundsätzlich zu erwarten. |
|
| |
| |
| |
 |
Weiter wichtige Kristalltypen haben i.a. mindesten zwei verschiedene
Atome in der Basis. | |
|
|
 |
Beispiele: NaCl Struktur: fcc, 2 Atome in der Basis; CsCl Struktur,
kub-prim., 2 Atome in der Basis; Zinkblende; fcc, 2 Atome in der Basis (die meisten Halbleiter) |
|
| |
| |
| |
| |
|
© H. Föll (MaWi 1 Skript)


