Minimization problems

4.7 Minimization problems

Remember 1D: $f(x)$ extreme value at $x_0$
$f(x)\ge f(x_0)$ for all $x$ close to $x_0\rightarrow\,x_0$-minimum
(similarly. $f(x)\le f(x_0)\to$ maximum)
(+ using $f''(x)$, i.e. -curvature information)

\[ \mbox{$x_0$-extremum}\Rightarrow f'(x_0)=0\wedge\left\{\begin{array}{ll}\mbox{if $f''(x_0)\lt0$}&\mbox{maximum}\\ \mbox{if $f''(x_0)\gt0$}&\mbox{minimum}\\ \mbox{if $f''(x_0)=0$}&\mbox{no decision,} \\ & \mbox{(saddle point?)} \end{array}\right. \]

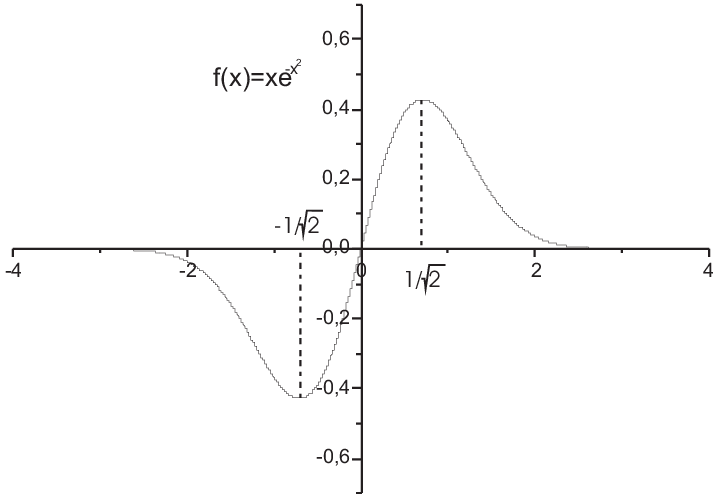
Example:

\begin{eqnarray*}f(x)&=&xe^{-x^2}\\ \rightarrow\,f'(x)&=&e^{-x^2}(1-2x^2)\to x_0=\pm\frac{1}{\sqrt{2}}\Leftrightarrow f'(x_0)=0\\ \rightarrow\,f''(x)&=&e^{-x^2}(2x^2-3)2x\\ \to f''(x_0)&=&e^{-\frac{1}{2}}\left(2\frac{1}{2}-3\right)2\frac{\pm1}{\sqrt{2}}\\&=&-4e^{-\frac{1}{2}}\frac{\pm1}{\sqrt{2}}=\pm2\sqrt{2}e^{-\frac{1}{2}} \end{eqnarray*}

\[\begin{array}{lcl}f''(+\frac{1}{\sqrt{2}})\lt0&\to&\mbox{max}\\f''(-\frac{1}{\sqrt{2}})\gt0&\to&\mbox{min}\end{array}\]

Example: $f:\mathbb{R}^N\to\mathbb{R}$
$N=2\;\;f(x,y)=x^2+y^2-2x-4y+5$
if $(x_0,y_0)$ with $f(x_0,y_0)\le f(x,y)$ for all $(x,y)$ exist then $(x,y)$ is a minimum:

\[f(x,y)=(x^2-2x+1)+(y^2-4y+4)=(x-1)^2+(y-2)^2\]

\[f(x,y)\ge0\;\to\;x_0=1\wedge\;y_0=2\;\mbox{is a minimum}\]

Derivatives: \begin{eqnarray*} \frac{\partial f}{\partial x}&=&2x-2\qquad\quad\frac{\partial f}{\partial x}=0\to x_0=1\\ \frac{\partial f}{\partial y}&=&2y-4\qquad\quad\frac{\partial f}{\partial y}=0\to y_0=2\\ &\rightarrow&\mbox{general feature ? YES!!}\end{eqnarray*}

Definition 41 local minimum $\vec{x}_0$ of $f:\mathbb{R}^N\to\mathbb{R}$ means that $f(\vec x)\ge f(\vec{x}_0)$ for all $\vec x\in\mathbb{R}^N$ ”close to” $\vec{x}_0$.
local maximum $\vec{x}_0$ of $f:\mathbb{R}^N\to\mathbb{R}$ means that $f(\vec x)\le f(\vec{x}_0)$ for all $\vec x\in\mathbb{R}^N$ ”close to” $\vec{x}_0$. Calculation of a (local) minimum or maximum in $N$-dimensions:
If $\vec x_0$ is a minimum or maximum then

\[ \vec\nabla f(\vec x_0)=\vec0,\;\mbox{i.e. }\;\frac{\partial f(\vec{x}_0)}{\partial x_k}=0\;\mbox{for all } k=1,\ldots,N\]

Note: this is a necessary condition and not always sufficient!! (same as in 1D)
Examples:

Minimum

\[f(x,y)=x^2+y^2\to\;\frac{\partial f}{\partial x}=2x,\;\frac{\partial f}{\partial y}=2y \quad\rightarrow\;(0,0) \mbox{ is a minimum since } f(x,y)\ge0 \mbox{ for all } (x,y)\]
Maximum

\[f(x,y)=-x^2-y^2\to\;\frac{\partial f}{\partial x}=-2x,\;\frac{\partial f}{\partial y}=-2x \quad\rightarrow\;(0,0) \mbox{ is a maximum since } f(x,y)\le0 \mbox{ for all } (x,y) \]

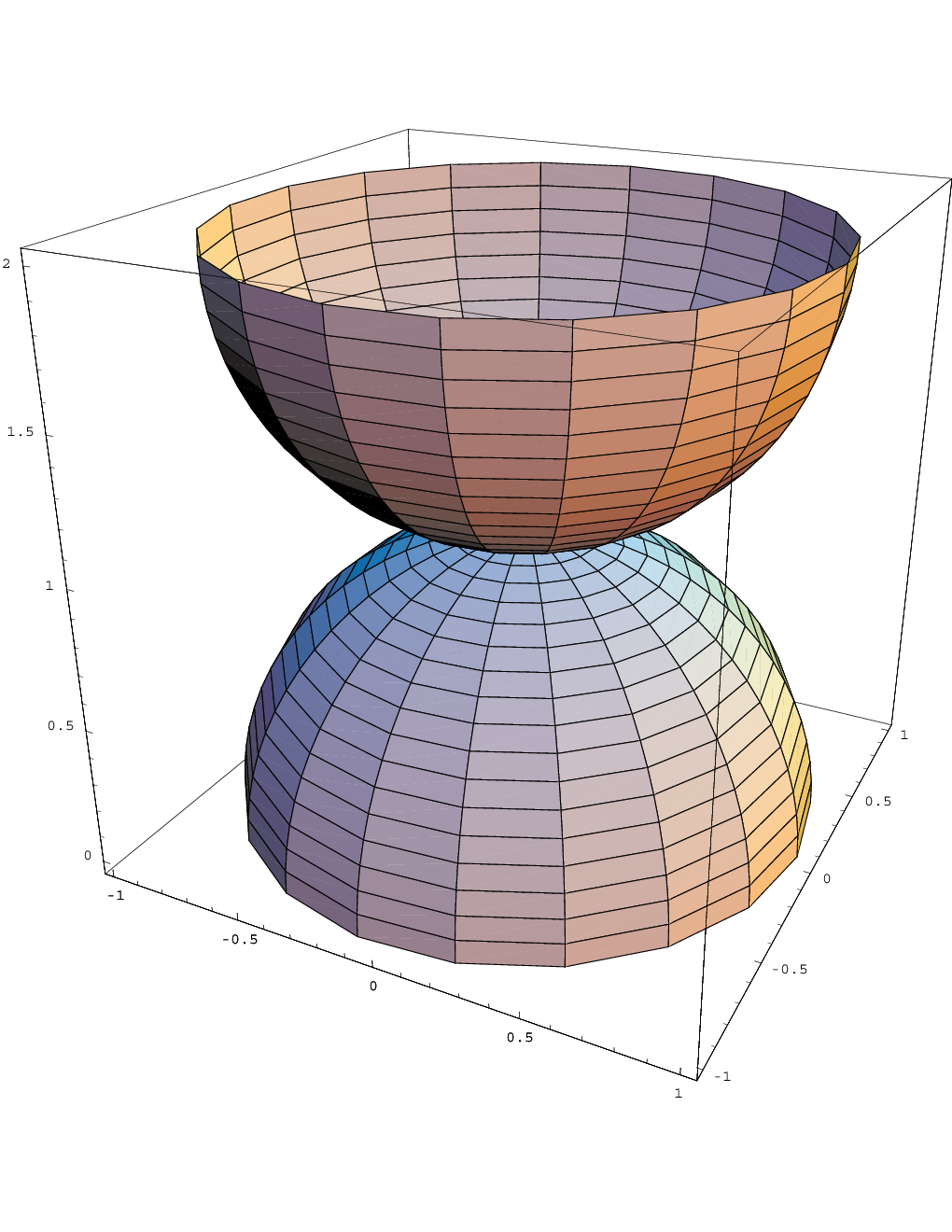
Saddle point

\begin{eqnarray*}f(x,y)=x^2-y^2&\rightarrow&\;\frac{\partial f}{\partial x}=2x,\;\frac{\partial f}{\partial y}=-2y\\ &\rightarrow&\vec\nabla f=\vec0 \mbox{ at }\vec{x}_0=\vect{0\\0}\end{eqnarray*}

But:

\[\left.\begin{array}{ccl} f(x,y=c)&=&x^2-c^2\to\infty\quad\mbox{for $x\to\infty$}\\ f(x=c,y)&=&c^2-y^2\to-\infty\quad\mbox{for $y\to\infty$}\end{array}\right\}\quad \mbox{no extreme} \]

$\rightarrow$”saddle point” at $(0,0)\;\Rightarrow\;$ second derivative?
$\vec\nabla f$ is the total derivative of $f:\mathbb{R}^N\to\mathbb{R}$
$\vec\nabla f$ is a function $\mathbb{R}^N\to\mathbb{R}^N$ since the gradient is a vector, thus

\[ \vec\nabla f=\vect{\frac{\partial f}{\partial x_1}\\\vdots\\\frac{\partial f}{\partial x_N}}\]

$\rightarrow\;$second (total) derivative is the (total) derivative of the gradient, i.e. it is an $N\times N$ Matrix $\tilde H$!

\[ \tilde H(\vec x)=\left(\begin{array}{ccc} \frac{\partial^2 f}{\partial x_1^2}&\cdots&\frac{\partial^2 f}{\partial x_1\partial x_N}\\ \vdots&\ddots&\vdots\\ \frac{\partial^2 f}{\partial x_N\partial x_1}&\cdots&\frac{\partial^2 f}{\partial x_N^2}\end{array}\right) \]

$\tilde H(\vec x)$ is symmetrical since $\frac{\partial^2 f}{\partial x_j\partial x_k}=\frac{\partial^2 f}{\partial x_k\partial x_j}$
$\tilde H(\vec x)$ is called the second derivative $f$ and has the name ”Hesse matrix ”