Functions of more than one variable

4.2 Functions of more than one variable

Functions may depend on more than one variable
Example: \begin{eqnarray*}f(x,y)&=&x^2+y^2\,\rightarrow\,\mbox{two variables, one function}\\ (x,y)^\top&=&\vec{r}\;\;:\;\;\rightarrow\, f(\vec{r})=(\vec{r})^2=x^2+y^2\end{eqnarray*}
”normal” situation in physics e.g. Hamilton function:

\[H(p,q)=\frac{p^2}{2m}+V(q)\;\mbox{$p$-momentum, $q$-position}\]

$N$ variables $x_1,\ldots,x_N\,\in\mathbb{R}$ vector $\vect{a_1\\\vdots\\x_N}=\vec{x}$
functions $f(x_1,\ldots,x_N)=f(\vec{x})\;\rightarrow$ $N$ dimensional area in $N+1$ D-space
2 Variables: $f(x,y)$ area, also niveau-lines
also possible, function has more than one component$\rightarrow$ curve in space
Example:

\[\vec{f}(t)=\vect{t^2\\2t}\quad t \in \mathbb{R}-\mbox{function itself is a vector, but depends on only one variable}\]

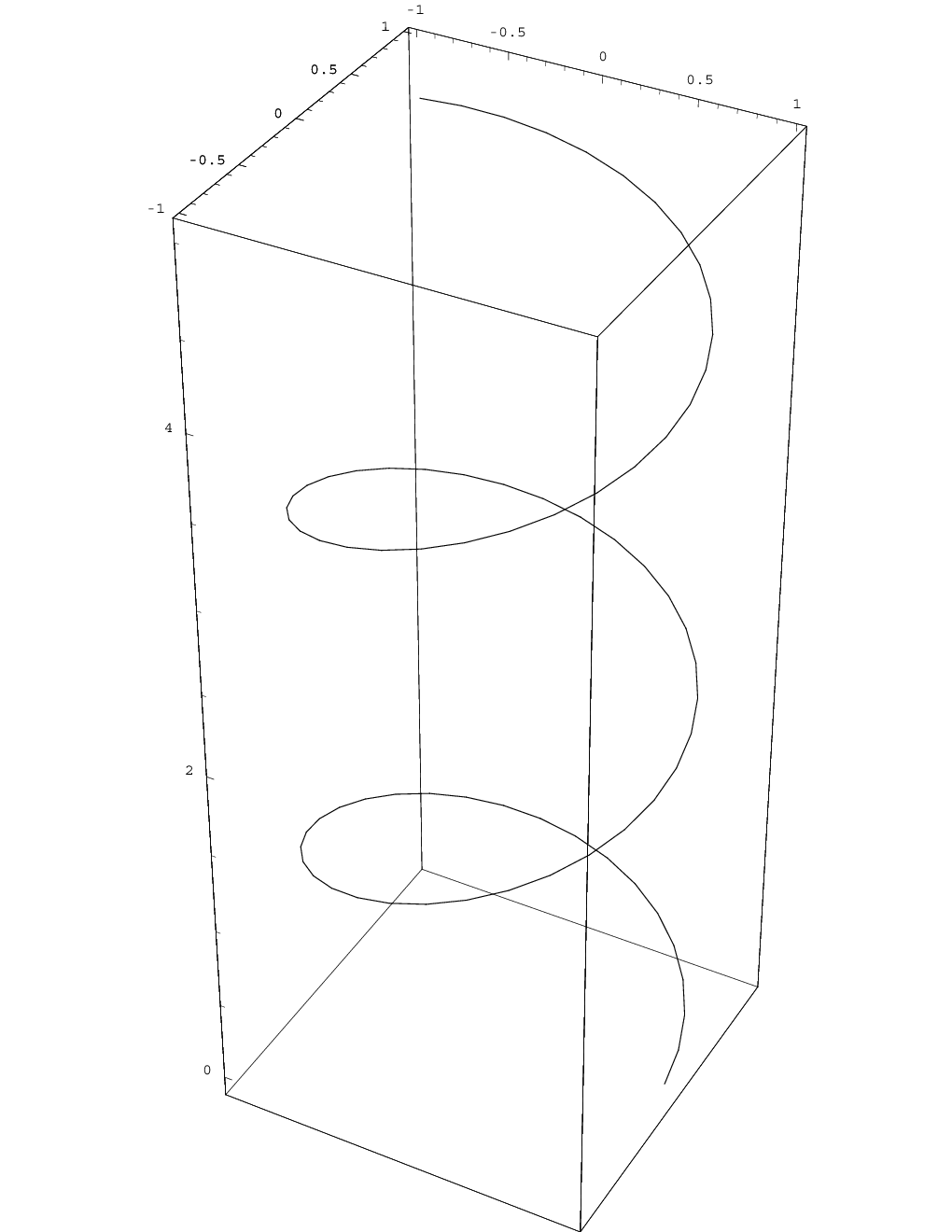
Other example: spiral in 3D Space

circle in x-y plane (projection)
$\vec{f}(t)=\vect{a\cos t\\a\sin t\\ct}\quad \text{ a, c, const., } t\in\mathbb{R}$

$M$-Dimensions:

\[\vec{f}(t)=\vect{f_1(t)\\\vdots\\f_M(t)}\rightarrow\,M \text{ dimensional curve.}\]

Moduls: $|\vec{f}(t)|^2=f_1^2(t)+\ldots+f_M^2(t)$ but this is not the length of the curve!

General case: $N$ variables and $M$ components

\[\vec{f}:\mathbb{R}^N\rightarrow\mathbb{R}^M\qquad\vec{x}=\vect{x_1\\x_2\\x_3\\\vdots\\x_N}\rightarrow\,\vect{f_1(x_1,\ldots,x_N)\\f_2(x_1,\ldots,x_N)\\\vdots\\f_M(x_1,\ldots,x_N)}=\underbrace{\vec{f}}_{\mbox{$M$-D-vector}}(\overbrace{\vec{x}}^{\mbox{$N$-D-vector}})\]

Examples:

Combination of circle and straight line $f:\mathbb{R}^2\quad\Rightarrow \quad \mathbb{R}^3$ \begin{eqnarray*} \vect{t_1\\t_2}&\Rightarrow&\vect{a\cos t_1\\a\sin t_1\\c t_2}\rightarrow\mbox{complicated function}\\ &&\left.\begin{array}{c}a\cos t_1\\a\sin t_1\end{array}\right\}\quad \mbox{circle, and }\quad c t_2\sim \mbox{a line}\end{eqnarray*}

Electric field as point sources at $\vect{0\\0\\0}:\vec{E}:\mathbb{R}^3\rightarrow\mathbb{R}^3$

\[\vec{E}(x,y,z)=\frac{q}{ 4 \pi \epsilon_0 (x^2+y^2+z^2)^{\frac{3}{2}} }\vect{x\\y\\z}=\vect{\frac{q}{4\pi\epsilon_0}\frac{x}{(\ldots)^{\frac{3}{2}}}\\\frac{q}{4\pi\epsilon_0}\frac{y}{(\ldots)^{\frac{3}{2}}}\\\frac{q}{4\pi\epsilon_0}\frac{z}{(\ldots)^{\frac{3}{2}}}}=\vect{E_x\\E_y\\E_z}\]

Modulus function: $\quad f:\mathbb{R}^N\quad\rightarrow\quad\mathbb{R}^1=\mathbb{R}$

\[\vect{x_1\\\vdots\\x_N}\quad\rightarrow\quad\left(x_1^2+x_2^2+\ldots+x_n^2\right)^{\frac{1}{2}}=f(x_1,\ldots,x_N)\]
Electric field, time dependent:

\[\vec{E}(x,y,z,t)=\vect{E_x(x,y,z,t)\\E_y(x,y,z,t)\\E_z(x,y,z,t)}\quad\vec{E}:\mathbb{R}^4\rightarrow\mathbb{R}^3\]