| \(\int\limits_0^\infty e^{-t^2}dt=\frac{\sqrt{\pi}}{2}\;\;\mbox{(limited)}\qquad\) | 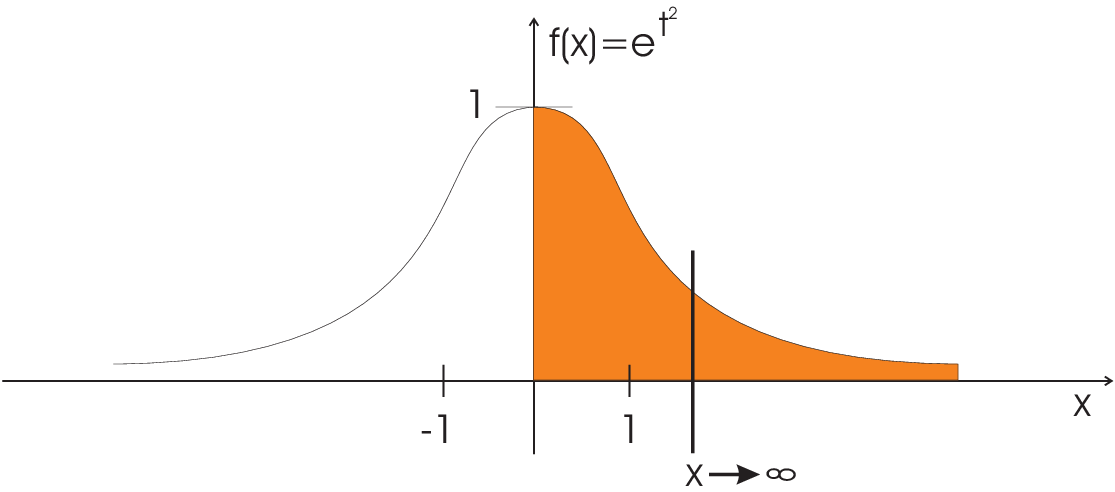 |
\(\int\limits_0^x f(t)dt\) is a function of \(x\) ”function
of the upper limit”
consider: \(f(t)=e^{-t^2}\) (Gauß-function or Gaussian)
| \[F(x)=\int\limits_0^x e^{-t^2}dt \quad.\] |
It is proven that there is no elementary function with
\(\frac{dF}{dx}=e^{-x^2}\)!
However one can show:
| \(\int\limits_0^\infty e^{-t^2}dt=\frac{\sqrt{\pi}}{2}\;\;\mbox{(limited)}\qquad\) |  |
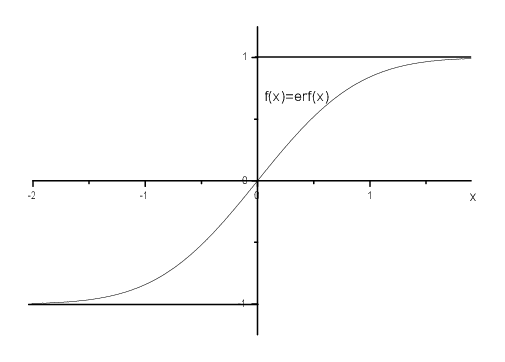
Definition 35 The error-function is defined by
| \[\mbox{erf}(x)=\frac{2}{\sqrt{\pi}}\int_0^x e^{-t^2}dt\] |
Power series: \begin{eqnarray*} e^{-t^2}&=&1-t^2+\frac{1}{2!}t^4-\ldots+\frac{1}{n!}t^{2n}-\ldots=\sum_{n=0}^\infty\frac{(-1)^n}{n!}t^{2n}\\ \Rightarrow\,\mbox{erf}(x)&=&\frac{2}{\sqrt{\pi}}\int\limits_0^x \sum\frac{(-1)^n}{n!}t^{2n}=\frac{2}{\sqrt{\pi}}\sum_{n=0}^\infty\frac{(-1)^n}{(2n+1)n!}t^{2n+1}=\frac{2}{\sqrt{\pi}}\left(t-\frac{t^3}{3\cdot1!}+\frac{t^5}{5\cdot2!}-\ldots\right) \end{eqnarray*}
Properties:
|
\begin{eqnarray*} \mbox{erf}(0)&=&0,\;\;\mbox{erf}(x)=-\mbox{erf}(-x)\\ \mbox{erf}(\infty)&=&\lim_{x\to\infty}\mbox{erf}(x)=1
\\ \mbox{erf}'(x)&=&e^{-x^2}\frac{2}{\sqrt{\pi}}\\ \mbox{erf}''(x)&=&-\frac{4}{\sqrt{\pi}} xe^{-x^2}\rightarrow x_0=0\;
\mbox{ only inflection point.}\end{eqnarray*}
|
The error-function is essential in probability theory:
| \(f(x)=\frac{1}{\sqrt{2 \pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\qquad\) | 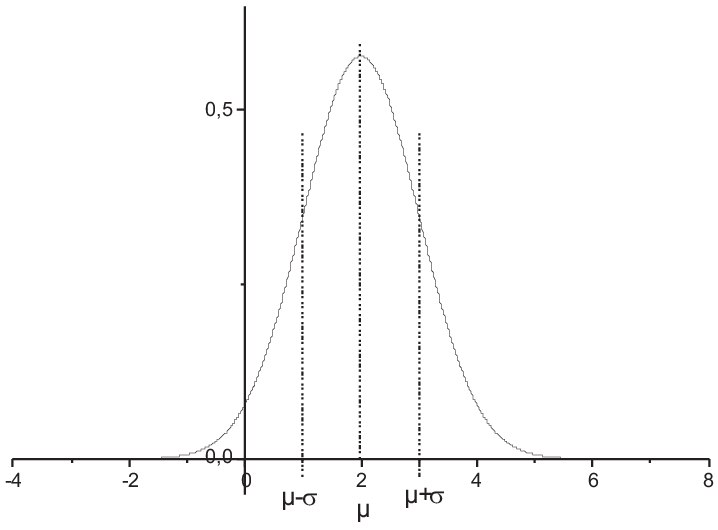 |
\(\hat=\) normal distribution of a random quantity characterized by two parameter: \(\mu,\;\;\sigma\)
Normalization:
| \[\int\limits_{-\infty}^{+\infty}f(x)dx=\frac{1}{\sqrt{2 \pi}\sigma}\int\limits_{-\infty}^{+\infty}e^{-\frac{(x-\mu)^2}{2\sigma^2}} dx = 1\] |
We prove this relation by calculating the square of the integral \begin{eqnarray*}\left(\int\limits_{-\infty}^{+\infty}e^{-x^2} dx\right)^2 & =& \int\limits_{-\infty}^{+\infty}\int\limits_{-\infty}^{+\infty} e^{-x^2} e^{-y^2} dx \; dy \\ &=&\int\limits_{0}^{2\pi}\int\limits_{0}^{+\infty}e^{-r^2} \;r\; dr\; d\varphi \quad \mbox{(using zylindrical coordinates)} \\ &=&\frac{1}{2}\int\limits_{0}^{2\pi}\int\limits_{0}^{\infty}e^{-z}\; dz\; d\varphi \quad \mbox{(substitution: $z = r^2$)}\\ &=& - \pi \left. \quad e^{-z} \right|_0^\infty = \pi \end{eqnarray*}
\(\mu:\) mean value of \(x\)
| \[\int\limits_{-\infty}^{+\infty}x f(x)dx=\frac{1}{\sqrt{2 \pi}\sigma}\int\limits_{-\infty}^{+\infty}(x-\mu) e^{-\frac{(x-\mu)^2}{2\sigma^2}} dx + \frac{1}{\sqrt{2 \pi}\sigma}\int\limits_{-\infty}^{+\infty}\mu e^{-\frac{(x-\mu)^2}{2\sigma^2}} dx = \mu\] |
\(\sigma:\) variance, standard deviation of \(x\) from the mean value \(\mu\) \begin{eqnarray*}\int\limits_{-\infty}^{+\infty}(x-\mu)^2f(x)dx & = & \frac{1}{\sqrt{2 \pi}\sigma}\int\limits_{-\infty}^{+\infty}(x-\mu)^2e^{-\frac{(x-\mu)^2}{2\sigma^2}}dx\\ & = & \frac{1}{\sqrt{2 \pi}\sigma}\int\limits_{-\infty}^{+\infty} \sigma^2 (x-\mu) \frac{(x-\mu)}{\sigma^2}e^{-\frac{(x-\mu)^2}{2\sigma^2}}dx\\ & = & \frac{1}{\sqrt{2 \pi}\sigma}\left\{ \left. - \sigma^2 (x-\mu) e^{-\frac{(x-\mu)^2}{2\sigma^2}} \right|_{-\infty}^{+\infty} + \int\limits_{-\infty}^{+\infty} \sigma^2 e^{-\frac{(x-\mu)^2}{2\sigma^2}}dx\right\}\\ & = & 0 + \sigma^2 \frac{1}{\sqrt{2 \pi}\sigma} \int\limits_{-\infty}^{+\infty} e^{-\frac{(x-\mu)^2}{2\sigma^2}}dx\\ & = & \sigma^2\end{eqnarray*}
\(\sim\)67%
of all values of the random variable x are with the interval \(\left[\mu-\sigma,\mu+\sigma\right]\)
\(\sim\)95% are in \(\left[\mu-2\sigma,\mu+2\sigma\right]\)
\(f(x)\)
probability density \(\rightarrow\) probability?
The probability that a value \(x\) in the interval \(\left[a,b\right]\) is given by: \begin{eqnarray*}P(a\le
x\le b)&=&\frac{1}{\sqrt{2\pi}\sigma}\int\limits_a^b e^{-\frac{(t-\mu)^2}{2\sigma^2}}dt\\ \mbox{defining: }\;\Phi(x)&=&\frac{1}{\sqrt{2\pi}}\int\limits_{-\infty}^x
e^{-\frac{t^2}{2}}dt=\frac{1}{2}\left[\mbox{erf}(\frac{x}{\sqrt{2}})+1\right]\\ \mbox{we get: }\;P(a\le x\le b)&=&\Phi\left(\frac{b-\mu}{\sigma}\right)-\Phi\left(\frac{a-\mu}{\sigma}\right)\end{eqnarray*}
© J. Carstensen (Math for MS)