\(\det(\tilde{A})\neq0\qquad\qquad\Rightarrow\qquad\) regular matrix
\(\tilde{A}=\tilde{A}^\top\qquad\quad\Rightarrow\qquad\) symmetric matrix \(a_{jk}=a_{kj}\;\) example \(\left(\begin{array}{ccc}1&0&4\\0&2&2\\4&2&3\end{array}\right)\)
\(\tilde{A}=-\tilde{A}^\top\qquad\Rightarrow\qquad\) anti-symmetric matrix \(a_{jk}=-a_{kj}\), in particular \(a_{jj}=0\Rightarrow \mbox{tr}(\tilde A)=0\)
\(\tilde{A}=\tilde{A}^+\qquad\quad \Rightarrow\qquad\) self-adjoined matrix
or Hermite-matrix ,
this means:
\(\tilde{A}=\overline{(\tilde{A}^\top)}, \; a_{jk}=\overline{a_{kj}}\;\)
example: \(\tilde{A}=\left(\begin{array}{ccc}1&2&-i\\2&2&1-i\\i&1+i&3\end{array}\right)\),
if \(\tilde
A\) is real then (ii) and (iv) are equivalent. \(\rightarrow\) diagonal elements of a Hermite-matrix are real,
because of \(a_{jj}=\overline{a_{jj}}\). The determinant is also real, i.e. \(\det(\tilde{A})\in\mathbb{R}\)
if \(\tilde A\) is a Hermite matrix.
\(\tilde{A}=-\tilde{A}^+\qquad\Rightarrow\quad\) anti-Hermite matrix (\(\rightarrow\) diagonal elements vanish) in particular \(a_{jj}=0\Rightarrow \mbox{tr}(\tilde A)=0\)
\(\tilde{A}^\top=\tilde{A}^{-1}\qquad\Rightarrow\quad\) \(\tilde
A\) is called orthogonal (real case) \(\tilde A\tilde{A}^\top=\tilde{A}^\top\tilde{A}=\tilde{I}\) if \(\tilde{A}\) is complex than \(\tilde{A}^+=\tilde{A}^{-1}\) means that A is ”unitary”. Properties of orthogonal matrices: \(\det(\tilde{A})=\pm1\)
(follows from \(\det(\tilde{A})=\det(\tilde{A}^\top)\) and \(\det(\tilde{A}\tilde{A}^\top)=\det(\tilde{A})\det(\tilde{A}^\top)\))
if \(\tilde{A}\) and \(\tilde B\) orthogonal, then \(\tilde{A}\cdot\tilde{B}=\tilde{C}\)
is also orthogonal.
Example: rotation around z-axis
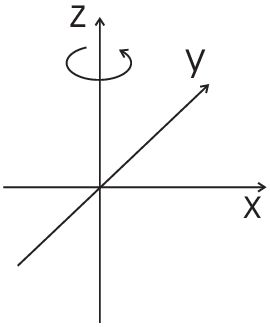
|
\begin{eqnarray*}\tilde{A}&=&\left(\begin{array}{ccc}\cos\phi&\sin\phi&0\\-\sin\phi&\cos\phi&0\\0&0&1\end{array}\right)\\
\rightarrow\;\tilde{A}^\top & = & \left(\begin{array}{ccc}\cos\phi&-\sin\phi&0\\\sin\phi&\cos\phi&0\\0&0&1\end{array}\right)\\
\Rightarrow\;\tilde{A}\tilde{A}^\top & = & \left(\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1\end{array}\right)\quad\mbox{since
$\quad \cos^2\phi+\sin^2\phi=1$}\end{eqnarray*}
|
Test:
| \[\det(\tilde{A})=1\left|{\genfrac{}{}{0pt}{}{\cos\phi}{-\sin\phi}}{\genfrac{}{}{0pt}{}{\sin\phi}{\cos\phi}}\right|=+1\;\;\mbox{o.k.}\] |
| \[\tilde{A}=\left(\begin{array}{cccc}a_{11}&0&\cdots&0\\0&\ddots& &0\\\vdots& &\ddots&\vdots\\0&0&\cdots&a_{NN}\end{array}\right)\] |
\(\det(\tilde A)=a_{11}\cdot a_{22}\cdot\ldots\cdot a_{NN}\) for diagonal matrix \(\tilde A\)