TTT Diagrams

2. Theory

Derivation of the equation

In this module I supposedly will show how to calculate TTT diagrams. It is an easy module for me because I have a message: forget it!

Calculating real TTT diagrams is beyond my skills. Even for simple but real materials it is not an easy task. That's also the reason why pretty much all real TTT or CCT diagrams have been experimentally determined.
All I'm going to do is to derive the most simple approximation to the problem, the celebrated Avrami equation, or to give it is's full name, the Johnson-Mehl-Avrami-Kolmogorov equation">Johnson-Mehl-Avrami-Kolmogorov (JMAK) equation. Those guys did not work together. Melvin Avrami published a number of papers to the topic around 1940, but the others had similar ideas around the same time or actually a bit earlier and credit must go to all even so Mehl is the most prominent one of the bunch¹⁾

We look on some g ® a transformation and generally assume that the transformation is finished after some time t. The JMAK equation gives us the transformed fraction f(t) as a function of time t and the relevant transformation parameters. It is based on a number of (not very realistic) assumptions:

Nucleation occurs randomly and homogeneously over the entire untransformed (= g ) portion of the material.
The growth rate or the velocity of the precipitate interface does not depend on the extent of the transformation.
Growth occurs at the same rate in all directions; i.e. nuclei always grow into spheres.

We start by assuming that the concentration N of nuclei increases by the constant generation rate dN/dt = G_N. They grow into spherical precipitates because the interface between the a precipitate and the g matrix moves outward with a constant velocity v.
The precipitates only stop growing if they hit each other (the polite word is "impinge"). We will neglect this for starters. In other words: we first look at unrestricted growth

We need to introduce two time scales. The first one is the regular time t. The second one measures the time in which precipitates grow and is denoted by t. It starts as soon as the precipitate is nucleated. Since precipitates are nucleated all the time, they all start growing at different times t but always at their own t = 0.

The (differential) number of nuclei that appear during a time interval dt in a volume V then is d N = G · V · dt; V is the volume of the material

The nuclei grow spherically and their interface moves into the g matrix with a velocity v that we also assume to be constant. After a nuclei appeared and started to grow, its radius r(t) will be speed times growing time or r = v · (t – t )

The additional (differential) volume dV_ur of the unrestrictedly growing phase a during a time interval dt then is given by:

		Volume of spheres					Generation of spheres
dV_{a, ur}	=	æ ç è	4 p 3	v³ · (t – t)³	ö ÷ ø	·	æ ç è	G · V · dt		ö ÷ ø

Integration from t = 0 to t = t will give the total volume of a and thus the amount transformed after the time t has elapsed. We get

V_{a, ur}	=	p 3	· G · V · v³ · t⁴

This can't be correct, however. As the fraction of a increases, more and more precipitates can't grow anymore because they encounter other ones. You can transform a g region only once, and if another precipitate has already done that, growth must stop as soon as two precipitates impinge on each other.

If we look at some arbitrary time t, the volume that has really been transformed from g to a is just V_a , without the index "ur". Expressed as a fraction of the total volume V it is V_a/V.

We now need to make the next assumption: At every time increment the really transformed differential volume dV_a is directly proportional to the differential volume dV_{a, ur} that we would get without restrictions, and to the volume fraction of the not yet transformed g phase, which is simply 1 – (V_a /V). This gives us

dV_a,	=	dV_{a, ur} ·	1 – (V_a/V)

1 1 – (V_a/V)	dV_a,	= –	dV_{a, ur}

Integrating both sides gives

ln { 1 – (V_a/V) }	= –	V_{a, ur} V

Inserting the expression for V_{a, ur} from above gives the final result, the JMAK equation in its most simple form:

			= 1 – exp–	K · t ⁿ
V_a/V	=	fraction of transformed volume	= 1 – exp–	æ ç è	p · G · v³ · t⁴ 3	ö ÷ ø

In the generalized version of the JMAK equation we have two constants, K and n, which we have calculated for a case where all the assumptions made would be valid. Such a hypothetical case is not very realistic, however. For realistic cases, we can expect that the general structure of the JMAK equation will stay intact but that the values of K and n will differ from the calculated values.

That the general structure of the JMAK equation will stay intact is clear from looking at the graph of that equation:

Graph of Johnson-Mehl-Avrami-Kolmogorov equation

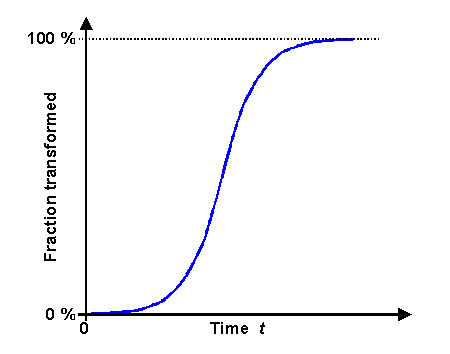Graph of the Johnson-Mehl-Avrami-Kolmogorov equation

	Working with the Johnson-Mehl-Avrami-Kolmogorov equation
	First, let's recall that we wanted to compute TTT diagrams and not just transformation rates. With the JMAK equations we can do this. All we need to know is the temperature dependence of the of the nuclei generation rate and of the interface speed, i.e. G(T) and v(T). Then we calculate the time needed to transform a certain fraction - 1 %, 50 %, 99 % - for a given temperature. This produces the corresponding curve in a TTT diagram. Note that you never try calculate the 0 % or 100 % curves because you know that they are asymptotic limits for infinitely long times and thus outside the scope of the equation
		Of course, before we start this undertaking, it would be good to know if the JMAK equation is actually good enough for the problems at hand. Well - what do you think? It is not good enough, of course, what with all those rather unrealistic assumptions and approximations. On the other hand, as pointed out above, it can't be too bad. A real transformation curve cannot look too different from the one given by the JMAK equation.
		The first parameter to give a close look is the exponent n, giving the n-th power of the time t. We have n = 4 if we assume three-dimensional growth of spherical precipitates. We can now go and do two different things: We calculate n for other kinds of nucleation and growth geometries We measure the transformation rate of all kinds of transformations and see what we get for n if we fit the results to the (generalized) JMAK equation. What we will find is that n is smaller than 4 for two-dimensional or one dimensional growth and that the JMAK equation with properly fitted K and n does indeed describe measured data quite well in many case. What we also find if looking closely is that things are actually far more complicated. One needs to be careful when extracting numbers from the JMAK equation.
	Nevertheless, the way of thinking that produced the JMAK equation is sound, and it does open the way to calculating and in particular to understanding TTT and CCT diagrams. I do not know if anybody actually calculates real diagrams of these kinds, they usually result from: Qualitative considerations plus some numbers known. That produces the kinds of diagrams I have shown so far. Painstaking measurements done for well-known materials under controlled conditions. that produced the precise and complex diagrams you find a-plenty in special books compiled for the cognoscenti who actually work with those materials
		The next module of this series will give examples for both



	¹⁾	As far as I can tell, the relevant publications are: A. N. Kolmogorov, Statistical theory of crystallization of metals. (in Russian). Izvestia Akademia Nauk SSSR Ser. Mathematica (Izv. Akad. Nauk SSSR, Ser. Mat; Bull. Acad. Sci. USSR. Ser. Math)., 1, 1937, S. 355–359 W. A. Johnson, R. F. Mehl, Reaction kinetics in processes of nucleation and growth, Transactions of American Institute of Mining and Metallurgical Engineers (Trans. Am. Inst. Min. Metall. Eng.), 135, 1939, S. 416–458 M. Avrami, Kinetics of phase change. III: Granulation, Phase Change and Microstructure, Journal of Chemical Physics (J. Chem. Phys.), 9, 1941, S. 177–184 Kolmogorov was a Russian mathematician who worked and is known in statistics. Johnson was a graduate student; Mehl was his adviser. Avrami was a chemist and generalized this kind of approach.

TTT Diagrams

TTT Diagrams 4. Experimental Construction of TTT and Phase Diagrams