4.1.3 Classifications of Interactions and Types of Magnetism

Dia-, Para-, and Ferromagnetism

	We want to get an idea of what happens to materials in external magnetic fields. "Material", in contrast to a single atom, means that we have plenty of (possibly different) atoms in close contact, i.e with some bonding. We can distinguish two basic cases:
		1. The atoms of the material have no magnetic moment of their own. This is generally true for about one half of the elements; the ones with even atomic numbers and therefore an even number of electrons. The magnetic moments of the spins tends to cancel; the atoms will only have a magnetic moment if there is an orbital contribution. Of course, the situation may change if you look at ions in a crystal.
		2. At least some of the atoms of the material have a magnetic moment. That covers the other half of the periodic table: All atoms with an odd number of electrons will have one spin moment left over. Again, the situation may be different if you look at ionic crystals.
	Lets see what can happen if you consider interactions of the magnetic moments with each other and with a magnetic field. First, we will treat the case of solids with no magnetic moments of their constituents, i.e. diamagnetic materials.
		The following table lists the essentials
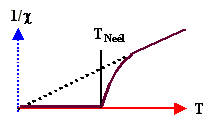
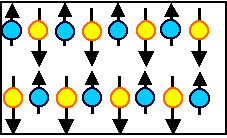
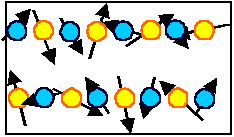
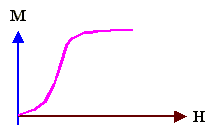
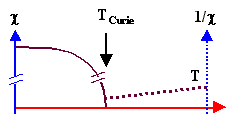
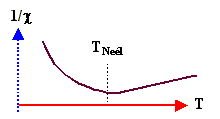
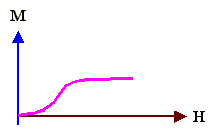
	Diamagnetic Materials Magnetic moment? No Internal magnetic interaction? None Response to external field Currents (and small magn. moments) are induced by turning on the field because the orbiting electrons are slightly disturbed. The induced magn. moments oppose the field. No temperature dependence Mechanism analogous to electronic polarisation in dielectrics, 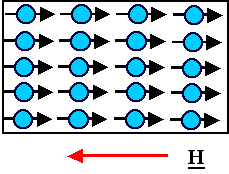The black arrows should be seen as being very short!!!! 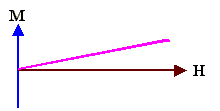Value of µr µr £» 1 in diamagnetic Small effect in "regular" materials µr = 0 in superconductors (ideal diamagnet) Value of B B £» µ0·H B = 0 in superconductors Typical materials All elements with filled shells (always even atomic number) all noble gases, H2, Cu, H2O, NaCl, Bi, ... Alkali or halogene ions

	Since you cannot expose material to a magnetic field without encountering a changing field strength dH/dt (either by turning on the field on or by moving the specimen into a field), currents will be induced that produce a magnetic field of their own.
		According to Lenz's law, the direction of the current and thus the field is always such as to oppose the generating forces. Accordingly, the induced magnetic moment will be antiparallel to the external field.
		This is called diamagnetism and it is a weak effect in normal materials.
	There is an exception, however: Superconductors, i.e. materials with a resistivity = 0 at low temperatures, will have their mobile charges responding without "resistance" to the external field and the induced magnetic moments will exactly cancel the external field.
		Superconductors (at least the "normal" ones (or "type I" as they are called) therefore are always perfectly field free - a magnetic field cannot penetrate the superconducting material.
		That is just as amazing as the zero resistance; in fact the magnetic properties of superconductors are just as characteristic for the superconducting state of matter as the resistive properties.
	There will be a backbone II module for superconductors in due time

	If we now look at materials where at least some of the atoms carry a permanent magnetic moment, we have to look first at the possible internal interactions of the magnetic moments in the material and then at their interaction with an external field. Two limiting cases can be distinguished.
		1. Strong internal interaction (i.e. interaction energies » kT, the thermal energy). Ferromagnetism results
		2. No or weak interaction. We have paramagnetic materials.
	The first case of strong interaction will more or less turn into the second case at temperatures high enough so that kT >> interaction energy, so we expect a temperature dependence of possible effects. A first classification looks like this:
	Paramagnetic and Ferromagnetic Materials Magnetic moment? Yes Internal agnetic interaction? Strong Weak Ordered regions? Yes No This example shows a ferrimagnetic material Ordered magnetic structures that are stable in time. Permanent magnetization is obtained by the (vector) sum over the individual magnetic moments. Example for a paramagnetic material Unordered magnetic structure, fluctuating in time. Averaging over time yields no permanent magnetization Response to external field A large component of the magnetic moment may be in field direction Small average orientation in field direction. Mechanism fully analogous to orientation polarization for dielectrics Kinds of ordering Many possibilities. Most common are ferro-, antiferro-, and ferrimagnetism as in the self-explaining sequence below: Value of µr µr >> 1 for ferromagnets µr » 1 for anti-ferromagnets µr > 1 for ferrimagnets µr ³»1 T-dependence Paramagnetic above Curie Temperature Weak T-dependence Paramagnetic materials (at room temperature) Mn, Al, Pt, O2(gas and liquid), rare earth ions, ... Ferromagnetic materials (with Curie- (or Neél) T) Ferro elements: Ferro technical: Ferri: Antiferro: (no technical uses) Fe (770 0C), Co (1121 0C), Ni (358 0C), Gd (16 0C) "AlNiCo", Co5Sm, Co17Sm2, "NdFeB" Fe3O4, MnO (116 0C), NiO (525 0C), Cr (308 0C)

	This table generated a lot of new names, definitions and question. It sets the stage for the dealing with the various aspects of ferromagnetism (including ferri- and anti-ferro magnetism as well as some more kinds of internal magnetic ordering. A few examples of ferromagnetic materials are given in the link.
		There might be many more types of ordering: Any fixed relation between two vectors qualify. As an example, moment 2 might not be parallel to moment 1 but off by x degrees; and the succession of many moments might form a spiral pattern.
		If you can think of some possible ordering (and it is not forbidden by some overruling law of nature), it is a safe bet that mother nature has already made it in some exotic substance. But, to quote Richard Feynman:
		"It is interesting to try to analyze what happens when a field is applied to such a spiral (of magnetic ordering) - all the twistings and turnings that must go on in all those atomic magnets. (Some people like to amuse themselves with the theory of these things!)" (Lectures on Physics, Vol II, 37-13; Feynmans emphasizes).
	Well, we don't, and just take notice of the fact that there is some kind of magnetic ordering for some materials.
		As far as the element are concerned, the only ferromagnets are: Fe, Ni, and Co. (Mn almost is one, but not quite).
		Examples for antiferromagnets include Cr, ....
		And there are many, many compounds, often quite strange mixtures (e.g. NdFeB or Sm2Co17), with remarkable and often useful ferro-, ferri, antiferro, or,..., properties.

	Temperature Dependence of Magnetic Behavior
	How do we distinguish an antiferromagnetic material from a paramagnet or a diamagnet? They all appear not to be very "magnetic" if you probe them with a magnetic field.
		We have to look at their behavior in a magnetic field and at the temperature dependence of that behavior. Ordering the atomic magnetic moments is, after all, a thermodynamical effect - it always has to compete with entropy - and thus should show some specific temperature dependence.
		There are indeed quite characteristic curves of major properties with temperature as shown below.
		Magnetization M = M(H) Magnetic susceptibility cmag = cmag(T) Remarks For diamagnets the susceptibility is negative and close to zero; and there is no temperature dependence. For paramagnets, the susceptibility is (barely) larger than zero and decreases with T. Plotted as 1/c(T) we find a linear relationship. For ferromagnets the susceptibility is large; the magnetization increases massively with H. Above a critical temperature TCu, the Curie temperature, paramagnetic behavior is observed. Antiferromagnets are like paramagnets above a critical temperature TNe called Neél temperature. Below TNe the susceptibility is small, but with a T-dependence quite different from paramagnets. Ferrimagnets behave pretty much like ferromagnets, except that the effect tends to be smaller. The 1/c(T) curve is very close to zero below a critical temperature, also called Neél temperature. Just for good measure, the behaviour of one of the more exotic magnetic materials. Shown is a metamagnet, behaving like a ferro magnet, but only above a critical magnetic field strength.

	The question now will be if we can understand at least some of these observations within the framework of some simple theory, similar to what we did for dielectric materials
		The answer is: Yes, we can - but only for the rather uninteresting (for engineering or applications) dia- and paramagnets.
		Ferro magnets, however, while extremely interesting electronic materials (try to imagine a world without them), are a different matter. A real understanding would need plenty of quantum theory (and has not even been fully achieved yet); it is far outside the scope of this lecture course. But a phenomenological theory, based on some assumptions that we do not try to justify, will come straight out from the theory of the orientation polarization for dielectrics, and that is what we are going to look at in the next subchapters.
		Questionaire Multiple Choice questions to 4.1.3

© H. Föll (Electronic Materials - Script)