Hystereses Losses

	Finding the proper formula for the hystereses losses is most easily done by considering the following situation:
			We have a single loop of wire around a doughnut of magnetic material with R = (average) radius of the doughnut or torus of the magnetic material. A current I flows through the wire loop.
			The magnetic field H generated by this arrangement is given by
			H  =  I 2pR

	This formula follows straight from the Maxwell equations; it is known as Ampères law.
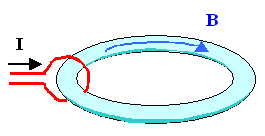
		The magnetic field H of the wire coil induces a magnetic flux B in the torus.
		If we now imagine that I changes suddenly , e.g. by DI in the time interval Dt, to a new constant value, the magnetic flux changes by DB, and a voltage U will be induced in the wire coil given by
		U =    A · DB Dt
		With A = cross-sectional era of the torus
	This is of course nothing but the well-known effect of self-inductance - you cannot turn on a current very quickly that is flowing through a large inductance.
		In our "experiment", however, we just keep the current at the new constant value - even against the effect of the induced voltage that opposes current flow in the wire.
		This requires that we cancel the effect of the induced voltage by raising the outside voltage accordingly. Since we are interested in power losses, we may also argue that we now need to supply power to the system for a while to be able to keep I  fixed. Note that in this kind of "experiment" we can make the wire with zero resistance, so no power is fed into the system as long as I does not change
	We need to maintain a current I against a voltage U; this requires the power PDB = U · I.
		Using our formulas from above (using I = 2pR · H) yields
		PDB  =  2pR · H · A · DB Dt
	Power is energy times time; for finding a useful material properties it is advantageous to calculate the energy E deposited in the magnetic material per unit volume
		Dividing by the volume V = 2pR · A and forming EDB = PDB · Dt gives
		EDB  =  H · DB
	The total energy deposited in an unit volume of the magnetic material during the time it takes to run through one cycle of the hystereses curve is obtained by integrating over a complete cycle, i.e.
		Ecycle  =  ? ó õ ? H · dB
		With slightly unclear boundaries at present. Lets look at this
		Since we are integrating over B; we rotate the hystereses curve to obtain the conventional "y - x" form:
		This is exactly the hystereses curve used before, we just replaced M by B which does not change the shape. For integrating once around the loop, we may start at the extreme - Br and integrate to the other end, i.e. to Bmax.
		This gives us the area shown in green which corresponds to the energy needed to change B from Br to Bmax.
		Now we continue the integration running backwards from - Bmax to Br. This gives us the small area corresponding to the green part outside the hystereses loop, however with a negative sign because we actually recover some energy stored in the magnetization of the material.
	In total we obtain just half of the area of the hystereses loop.
		The complete integral thus is simply the area contained in the hystereses loop.
	For hard magnetic materials with a roughly rectangular hystereses loop, the area and thus the energy dispersed in one cycle per unit volume is than approximately
		Ecycle  =  ó õ H · dB   »   2 ·HC · Br
		The total power loss than is the energy loss per cycle times the number of cycles, i.e.
		P   »   2 · f · HC · Br
		With f = frequency.
	This was the formula used in the main part.

With frame

4.3.5 Magnetic Losses and Frequency Behavior

© H. Föll (Electronic Materials - Script)