Bollmanns Interpretation of Franks Formula

	Franks formula relates the sum d of all Burgers vectors cut by a vector r (which is required to be in the plane of the boundary) to the (small) rotation angle a around an arbitrary polar vector l that generates the second crystal from the first one. It reads:
		d = (r x l)·a
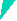	Franks formula at this point is a continuity equation, it gives a value of d for every a and r
		Burgers vectors, however, are discrete. This requires the vector d to be discrete, too.
		Since Burgers vectors are translation vectors of the lattice, d can only be a sum of Burgers vectors if l is a lattice vector so that the "b-plane", the plane perpendicular to l that contains the possible Burgers vectors, is a lattice plane, too (i.e. can be indexed with {hkl}, with h, k, l = integers). It contains lattice points that define the possible Burgers vectors in this plane.
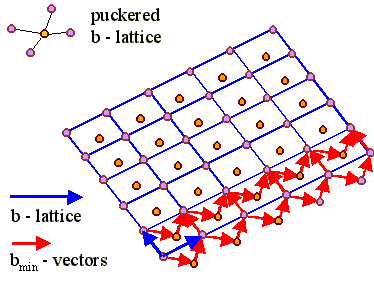
		Note that the Burgers vectors defined in this way must not necessarily be the shortest possible Burgers vectors bmin, i.e. the Burgers vectors of real dislocations. It is, however, always possible to decompose the b vectors of the -lattice into, e.g., a/2<110> type Burgers vectors of the fcc lattice. This may require bmin-vectors that are not contained in the b- plane - but all we have to do then is to imagine the b-plane to be "puckered" as shown below.
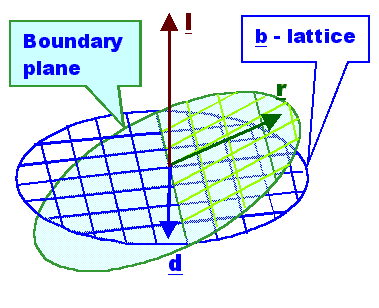
	On the plane of the boundary, an arbitrary r would intersect the projection of the b-lattice onto the boundary plane along the l-direction . In a schematic view we have the following situation:
	Franks formula can now be understood as a discrete imaging of points in a two-dimensional "Burgers vector space" onto a plane in real space.
		The Burgers vector count along r (after translating it to smallest possible vectors bmin) gives the number of dislocations that are found if going along r in the boundary plane. If even spacing is assumed, we also know the spacing in the particular direction given by r.
		The line direction of the dislocation is obtained by probing the whole two-dimensional grain boundary space by sweeping r around. What happens then can be understood in purely geometrical terms, as we will see.

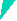	First of all it is important to realize that the b-lattice is simply the Moirée pattern of the superimposed two crystals obtained by rotating the {hkl} planes perpendicular to l on top of each other by a as shown below for three different as with a picture from Bollmanns book.
					In the whitish (bright) areas, there is a high degree of coincidence of lattice points, whereas in the black areas the misfit is largest. Whenever a vector from the origin crosses a black area to reach a whitish area again, the translation relative to a equivalent vector in the other lattice is just a lattice vector of the underlying plane, which is the b-plane in our definition.
					If the crystal now introduces a boundary, it will increase the whitish areas, the areas of best fit, and concentrate the misfit on the black areas, which correspond to the dislocations.
					Since the does not depend on its position along l (in other words: Which planes of the real crystals perpendicular to l we rotate relative to each other does not matter), we can extend it along the l direction. If we enclose the lattice points of the b-lattice in Wigner-Seitz cells, we obtain a kind of honeycomb structure.
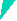	The decisive point now is that the boundary plane, which can have any position possible relative to l, intersects this "honeycomb" b-lattice somehow, for an cases we obtain the following picture (again taken from Bollmanns book):
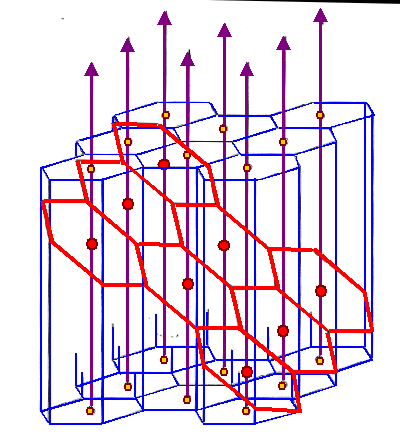					The b-lattice consists of the yellow lattice points. It is turned into the three-dimensional "honeycomb" lattice by introducing Wigner-Seitz cells (blue lines) and continuing it along the l direction (magenta arrows).
					An inclined boundary plane will have a dislocation wherever the boundary plan intersects the honeycombs. The resulting dislocation network is shown with red lines. The points of best fit Red points) are in the center of the network as it must be.
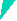	The final interpretation now is as follows:
		Wherever the boundary plane intersects a cell wall of the (three-dimensional) b-lattice, we have a dislocation with the Burgers vector as defined by the b-lattice. The lines defined by the intersection of the boundary plane and the cell walls then directly define the dislocation lines - we get a direct rendering of the dislocation network in the boundary.
		Of course, the geometry of the dislocation network obtained in this way depends on the kind of unit cell we chose for the "honeycomb" b-lattice. Wigner-Seitz cells, while universal, may not be best choice possible. But it is always possiblenow to "develop" the network obtained in a network with minimum energy by using the rules of dislocation interaction as in the example with the small angle twist boundary on a {111} plane.
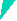	These and other complications need more considerations. However, remembering that Franks formula is an approximation and covers only small angle grain boundaries, it is not worth the effort to improve this limited theory. It is a better at this point approach to unleash the full power of O-lattice theory which contains franks formula as a special case.

	The concepts behind Franks formula are not easy and lead into deep water. Lets recapitulate the essential concept:
		The orientation relationship between the two crystals (expressed here as one rotation) always leads to a kind of Moirée pattern that can be identified as a Burgers vector lattice (b-lattice) describing the localized displacements necessary to match the two crystals on some boundary plane.
		The b-lattice can be extended to three dimensions (the "honeycomb" lattice for the case treated here). The cell walls of this three-dimensional lattice define the dislocation content of the boundary and the Burgers vectors encountered in crossing a wall.
		The intersection lines obtained by cutting the three-dimensional b-lattice with the boundary plane defines directly the dislocation network.

7.3.3 The Significance of the O-Lattice

Franks Formula