|
|
 |
Standardmethode |
|
 |
Messung des Konzentrationsprofils des diffundierenden
Teilchens, daraus (durch Lösung der zugehörigen
Differentialgleichungen der Fickschen Gesetze) Ermittlung des
Diffusionskoeffizienten. |
|
 |
Probleme: Geht nur bei meßbaren Profilen, daraus folgen
zwei Bedingungen.
- Viele Sprünge erforderlich, also Diffusion nur bei "hohen"
Temperaturen möglich
- Wie mißt man die Konzentration von z.B. Leerstellen,
Eigen-Zwischengitteratomen, oder überhaupt der Eigenatome die gesprungen
sind bei der Selbst-Diffusion; insbesondere bei sehr kleinen Konzentrationen?
|
| Tracermethoden
|
 |
Die Antwort insbesondere auf die 2. Frage liegt in
"Tracer" - Methoden. Die interessierten Atome werden markiert, indem
man ein radioaktives Isotop verwendet. Bei geeigneten Halbwertszeiten sind
minimalste Konzentrationen nachweisbar, da jeder einzelne Zerfall
meßtechnisch erfaßt werden kann. |
 |
Grundsätzliche Durchführung eines
Tracer-Experiments |
|
 |
Aufbringen einer dünnen Schicht des zu untersuchenden
Stoffes (durch Dünnschichtverfahren (Aufdampfen, Sputtern, Sol-Gel, ...))
auf die (saubere) Oberfläche des Kristalls. |
|
 |
Tempern bei der gewünschten Diffusionstemperatur für
eine bestimmte Zeitdauer. |
|
 |
Stufenweises Abtragen des Kristalls (idealerweise Atomlage um
Atomlage; z.B. durch Sputtern, anodische Oxidation und Ätzung,
Ultramikritom,..). |
|
 |
Messung der Radioaktivität jeder einzelnen Schicht. |
|
 |
Daraus, über die bekannte Halbwertszeit und die bekannte
Meßzeit, Berechnung der Zahl der in der Schicht vorhandenen Tracer Atome,
daraus Konzentrationsprofil. |
|
 |
Aus Konzentrationsprofil und Standardlösungen der
Diffusionsgleichungen folgt der Diffusionskoeffizient bei
einerTemperatur. |
|
 |
Wiederholung des Experiments bei einer anderen Temperatur. |
|
 |
Aus Arrhenius-Darstellung von D(T) folgt D* und
Aktivierungsenthalpie. |
 |
Grundsätzliches Problem bei
Tracerexperimenten |
|
 |
Der Tracer-Diffusionskoeffizient ist (bei Experimenten zur Selbstdiffusion)
nicht notwendigerweise der Diffusionskoeffizient der interessierenden
Teilchen (Alle Gitteratome, Zwischengitteratome, Leerstellen,
Doppel-Leerstellen, ...). Dies liegt daran, daß z.B. bei einem einfachen
Leerstellenmechanismus, die Sprünge des Traceratoms und die der Leerstelle
korrelliert sein können. Dies bedeutet, daß zwar die Leerstelle
völlig statistisch wandert - jeder Sprung trägt zum mittleren
Verschiebungsquadrat bei - nicht jedoch das Traceratom. |
|
 |
Beispiel: Einfacher Leerstellen-Mechanismus |
|
|
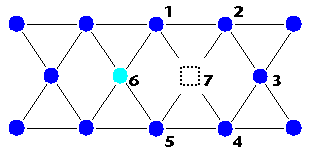 geht über in geht über in
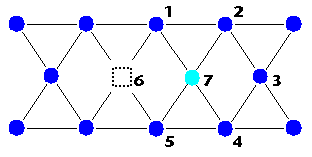 |
|
 |
Durch den Sprung der Leerstelle von 7 nach 6 ist das Traceratom von 6 nach
7 gehüpft, wo es jetzt sitzt. Während nun die Leerstelle in ihrem
nächsten Sprung mit gleicher Wahrscheinlicheit auf einen der 6 umliegenden
Plätze springt, wird das Traceratom mit höherer Wahrscheinlichkeit
wieder auf Platz 6 springen als auf einen der anderen Plätze. Denn dort
sitzt ja noch eine Leerstelle; für alle anderen Plätze muß erst
gewartet werden bis ein Leerstelle dort auftaucht. Der bevorzugte
Rücksprung verfälscht die Berechnung des mittleren
Verschiebungsquadrats, da Sprünge mit nachfolgendem Rücksprung nicht
beitragen. |
 |
Die Korrelationseffekte werden durch
denKorrelationskoeffizienten f berücksichtigt, der für den
betrachteten Mechanismus angegeben wird.
Beim einfachen Fall einer Selbstdiffusion über einen
Einfach-Leerstellen-Mechanismus ist f1V durch die Geometrie
bestimmt; in guter Näherung gilt |
|
 |
f1V = 1 - 2/z mit z
= Zahl nächster Nachbarn. |
 |
Für die Diffusionskoeffizienten gilt dann
|
|
 |
D1V(T) = über Tracerexperiment ermittelter
Diffusionskoeffizient der Leerstelle
= f1V D1V(SD)mit
D1V(SD) = Diffusionskoeffizient der
Selbstdiffusion |
 |
Der Korrelationskoeffizient ist - bei bekanntem
Mechanismus - berechenbar, und - wenn auch nur selten und mit Mühe - auch
meßbar. |
 |
Die Korrelationseffekte bei Fremdatomen, die
über einen Leerstellenmechanismus diffundieren, oder für andere
Mechanismen können komplizierter sein. |
|
 |
Bei einer Wechselwirkung zwischen Leerstelle und Fremdatom
springt jetzt auch die Leerstelle nicht mehr rein statistisch |
|
 |
Beim kick-out Mechanismus
wird das Tracer Atom schnell unbeweglich im Gitter liegen, dafür
diffundiert das herausgekickte Atom. |
 |
Beispiele für
Korrelationskoeffizienten bei einfachem Leerstellenmechanismen (nach
Seeger): |
|
|
| Gitterart |
KO - Zahl z |
f1V=1 - 2/z |
f1V Korrekt |
| Eindim. Kette |
2 |
0 |
0 |
| Zweidim. Gitter |
|
|
|
| hexagonale Kugelpackg. |
6 |
0.6666 |
0,56006 |
| quadratisch |
4 |
0,5 |
0,46694 |
| Dreidim. Gitter |
|
|
|
| kub. primitiv |
6 |
0,6666 |
0,65311 |
| Diamant |
4 |
0,5 |
0,5 |
| bcc |
8 |
0,75 |
0,72722 |
| fcc |
12 |
0,83 |
0,78146 |
|
Andere Methoden
für Messungen von Diffusionsparametern
|
 |
Es gibt sehr viele Methoden, einige werden in der
Analytik I und II behandelt. Hier stichwortartig eine Auswahl. |
 |
Direkte Messung der Konzentrationsprofile
eindiffundierter Fremdatome mit |
|
 |
SIMS (Secondary Ion Mass Spectroscopy) |
|
 |
RBS ( Rutherford Backscattering) |
|
 |
C(U) (und Tiefe) (Kapazitäts-Spannungsmessung
(gibt bei Halbleitern Ladungsrägerdichte und damit Dichte der (elektrisch
aktiven) Dotierelemente) |
 |
Lokale Messungen aus der Wachstumskinetik
von größeren Defekten, z.B. |
|
 |
Wachstum von Ausscheidungen, Stapelfehlern, etc |
|
 |
Diffusionshöfe um Korngrenzen |
 |
Abbildung Diffusionshöfe
sichtbar gemacht im ELYMAT
|
 |
Ausheilversuche. Hier werden atomare Fehlstellen, die
man "irgendwie" in hohen Konzentrationen eingefroren (=unbeweglich
festgehalten) hat, durch langsames Erwärmen beweglich gemacht. Da sie
verschwinden, oder zumindest agglomerieren wollen, kann man die Ausheilkinetik
durch die Messung einer geeigneten, mit atomaren fehlstellen korrelierten
Größe, bestimmen. |
|
 |
Das klassische Experiment erzeugt atomare Fehlstellen durch
"schonende" Bestrahlung mit Elektronen bei tiefen T - erzeugt
werden enge Frenkel Paare. Man heilt dann eine definierte Zeit bei einer
bestimmten Temperatur aus, und mißt dann (immer bei tiefer Temperatur)
den Restwiderstand. |
|
 |
Eine klassische Ausheilkurve sieht ungefähr wie folgt aus
|
|
|
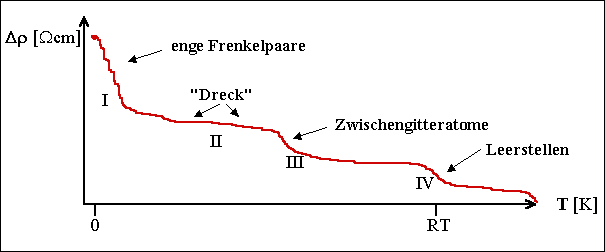 |
|
 |
Das Problem ist die Interpretation der Stufen durch eine
Ausheilreaktion. |
|
 |
Methoden, die einzelne Sprünge erfassen |
|
 |
Geht dann, wenn die atomaren Fehlstellen eine niedrige
Symmetrie haben - Beispiele: die Hantelform des Zwischengitteratoms., oder
Cin Fe (klassischer Snoek Effekt). |
|
 |
Klassisches Experiment: Material elastisch in einer Richtung
verformen (nicht zu kleine T; oder lange warten). Effekt: Alle Hanteln
orientieren sich in die Zugachse, die C-Atome sitzen bevorzugt in einer
der drei möglichen Lagen. |
|
|
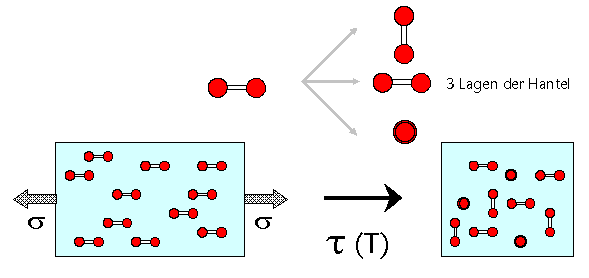
|
|
 |
Die Spannung wird plötzlich weggenommen: Außer einer unmittelbar
folgenden elastischen Komponente erfolgt jetzt noch eine langsam abklingende
T-abhängige Relaxation durch die Rückorientiereung der
atomaren Fehlstellen. In der Zeitkonstanten steckt die Sprungfrequenz. |
|
 |
Es existieren unzählige Varianten, insbesondere mit
periodischer Anregung |
 |
Weiterhin gibt es Methoden, die auf der
Zerstörung oder Errichtung einer inneren Ordnung durch Diffusion beruhen;
z.b. die Ausrichtung, bzw. der Zerfall einer Ausrichtung von (Kern)spins im
Magnetfeld. Der Nachweis erfolgt dann beispielsweise mit NMR (Nuclear
Magnetic Resonance). |
 geht über in
geht über in


